
分析 将a=-2代入h(x)=f(x)-g(x)中,求得h(x)的解析式,然后求出其导数,利用导数的性质结合题中已知条件便可求出b的取值范围;根据题意先求出φ(x)的解析式,然后分别讨论b的范围,确定函数的单调性,从而求出函数φ(x)的最小值即可.
解答 解:依题意:h(x)=ln x+x2-bx,h(x)在(0,+∞)上是增函数,
∴h′(x)=$\frac{1}{x}$+2x-b≥0对x∈(0,+∞)恒成立,
∴b≤$\frac{1}{x}$+2x,∵x>0,则$\frac{1}{x}$+2x≥2$\sqrt{2}$(当x═$\frac{\sqrt{2}}{2}$时取等号).
∴b的取值范围为(-∞,2$\sqrt{2}$].
设t=ex,则函数化为y=t2+bt,t∈[1,2],∵y=(t+$\frac{b}{2}$)2-$\frac{{b}^{2}}{4}$,
∴①当-$\frac{b}{2}$≤1,即-2≤b≤2$\sqrt{2}$时,函数y在[1,2]上为增函数,
当t=1时,ymin=b+1.
②当1<-$\frac{b}{2}$<2,即-4<b<-2时,当t=-$\frac{b}{2}$时,ymin=-$\frac{{b}^{2}}{4}$.
③当-$\frac{b}{2}$≥2,即b≤-4时,函数y在[1,2]上为减函数,当t=2时,ymin=4+2b.
综上所述,当-2≤b≤2$\sqrt{2}$时,φ(x)min=b+1;
当-4<b<-2时,φ(x)min=-$\frac{{b}^{2}}{4}$;
当b≤-4时,φ(x)min=4+2b.
点评 本题主要考查了利用导数求闭区间上函数的最值和函数的单调性,考查了学生的计算能力和对函数的综合掌握,解题时注意分类讨论的数学思想的运用,是各地高考的常考题,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | a+b<ab | B. | $\frac{b}{a}$+$\frac{a}{b}$>2 | C. | ab<b2 | D. | a2<b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
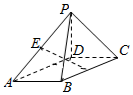 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥底面ABCD,PD=1,PB=PC=BC=$\sqrt{2}$,点E,F分别是PA,BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥底面ABCD,PD=1,PB=PC=BC=$\sqrt{2}$,点E,F分别是PA,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
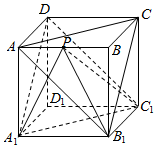
| A. | 平面ACB1∥平面A1C1D,且两平面的距离为$\frac{{\sqrt{3}}}{3}$ | |
| B. | 点P在线段AB上运动,则四面体PA1B1C1的体积不变 | |
| C. | 与所有12条棱都相切的球的体积为$\frac{{\sqrt{2}}}{3}$π | |
| D. | M是正方体的内切球的球面上任意一点,N是△AB1C外接圆的圆周上任意一点,则|MN|的最小值是$\frac{{\sqrt{3}-\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com