练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】阅读下面材料：

    根据两角和与差的正弦公式，有

    ------①

    ------②

    由①+② 得------③

    令有

    代入③得．

    （Ⅰ）类比上述推证方法，根据两角和与差的余弦公式，证明:

    ;

    （Ⅱ）若的三个内角满足,试判断的形状．

    【答案】（1）根据两角和差的余弦公式可以得到结论，

    （2）为直角三角形

    【解析】试题分析：解法一：(Ⅰ)因为， ①

    ， ② 2分

    ①-② 得. ③ 3分

    令有，

    代入③得. 6分

    (Ⅱ)由二倍角公式, 可化为

    , 8分

    即. 9分

    设的三个内角A,B,C所对的边分别为，

    由正弦定理可得. 11分

    根据勾股定理的逆定理知为直角三角形. 12分

    解法二：(Ⅰ)同解法一.

    (Ⅱ)利用(Ⅰ)中的结论和二倍角公式, 可化为

    ， 8分

    因为A,B,C为的内角，所以，

    所以.

    又因为，所以,

    所以.

    从而. 10分

    又因为,所以，即.

    所以为直角三角形. 12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某城市上年度电价为0.80元/千瓦时，年用电量为千瓦时.本年度计划将电价降到0.55元/千瓦时～0.7元/千瓦时之间，而居民用户期望电价为0.40元/千瓦时（该市电力成本价为0.30元/千瓦时)，经测算，下调电价后，该城市新增用电量与实际电价和用户期望电价之差成反比，比例系数为.试问当地电价最低为多少元/千瓦时，可保证电力部门的收益比上年度至少增加20%.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}的前n项和记为Sn ， a1=2，an+1=Sn+2（n∈N*）．
    （Ⅰ）求{an}的通项公式；
    （Ⅱ）求数列{nan}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知y=f（x）（x∈R）是偶函数，当x≥0时，f（x）=x2﹣2x．
    （1）求f（x）的解析式；
    （2）若不等式f（x）≥mx在1≤x≤2时都成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，底面为等边三角形， .

    （Ⅰ）求三棱锥的体积；

    （Ⅱ）在线段上寻找一点，使得，请说明作法和理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    （1）判断函数的奇偶性；

    （2）求证：函数在为单调增函数；

    （3）求满足的的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在区间上的值域.

    (1)求的值；

    (2)若不等式在上恒成立，求实数的取值范围；

    (3)若函数有三个零点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，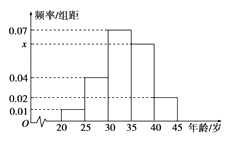

    （1）求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在 岁的人数；
    （2）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为 ，求 的分布列及均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E： 的左、右焦点分别为F1、F2 ， 离心率 ，P为椭圆E上的任意一点（不含长轴端点），且△PF1F2面积的最大值为1．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）已知直x﹣y+m=0与椭圆E交于不同的两点A，B，且线AB的中点不在圆 内，求m的取值范围．

    查看答案和解析>>

    同步练习册答案