
【题目】已知函数![]() 是单调递增函数,其反函数是
是单调递增函数,其反函数是![]() .
.
(1)若![]() ,求
,求![]() 并写出定义域
并写出定义域![]() ;
;
(2)对于⑴的![]() 和
和![]() ,设任意
,设任意![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)已知函数![]() 和
和![]() 的图象有交点,求证:它们的交点一定在直线
的图象有交点,求证:它们的交点一定在直线![]() 上.
上.
【答案】(1)![]() ,
,![]() ;(2)证明见详解;(3)证明见详解.
;(2)证明见详解;(3)证明见详解.
【解析】
(1)根据反函数的求解过程,即可求得![]() ,再求原函数值域,即为反函数的定义域;
,再求原函数值域,即为反函数的定义域;
(2)根据(1)中所求,用分析法将不等式进行不断转换,即可证明;
(3)根据互为反函数的两个函数的特点,以及函数单调性,即可证明.
(1)因为![]() ,故可得
,故可得![]() ,又因为
,又因为![]()
故![]() ,故
,故![]() ;
;
又因为![]() 在
在![]() 时,单调递增,故其值域为
时,单调递增,故其值域为![]()
故![]() 的定义域为
的定义域为![]() ;
;
综上所述:![]() ,
,![]() .
.
(2)由(1)可知![]() ,
,![]()
要证![]()
即证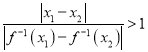
也就是证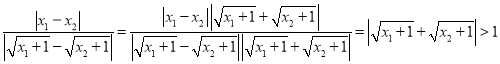
因为![]() ,故
,故![]() ,则
,则![]() ,同理可得
,同理可得![]()
故![]() 成立,
成立,
则原不等式![]() 成立,即证.
成立,即证.
(3)证明:设![]() 是函数
是函数![]() 与
与![]() 的交点,
的交点,
故可得![]()
故可得![]()
即![]() 过点
过点![]() 和
和![]()
又因为![]() 是单调第增函数,
是单调第增函数,
故当![]() 时,
时,![]() ,即
,即![]() ,这与题设矛盾;
,这与题设矛盾;
当![]() 时,
时,![]() ,即
,即![]() ,这也与题设矛盾;
,这也与题设矛盾;
当![]() 时,
时,![]() ,即
,即![]() ,满足题意.
,满足题意.
综上所述,若![]() 与
与![]() 有交点,则交点一定在直线
有交点,则交点一定在直线![]() 上,即证.
上,即证.


科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于点B、C,经过B、C两点的抛物线
轴分别相交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一交点为A,顶点为P,且对称轴为直线
轴的另一交点为A,顶点为P,且对称轴为直线![]() .
.
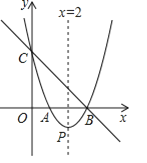
(1)求该抛物线的函数表达式;
(2)连结AC.请问在![]() 轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系. 已知曲线的极坐标方程为
轴的正半轴为极轴建立极坐标系. 已知曲线的极坐标方程为![]() ,直线 的参数方程为
,直线 的参数方程为 (
(![]() 为参数).
为参数).
(I)分别求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(II)设曲线![]() 和直线
和直线![]() 相交于
相交于![]() 两点,求弦长
两点,求弦长![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校拟建一块五边形区域的“读书角”,三角形区域ABE为书籍摆放区,沿着AB、AE处摆放折线形书架(书架宽度不计),四边形区域为BCDE为阅读区,若∠BAE=60°,∠BCD=∠CDE=120°,DE=3BC=3CD=![]() m.
m.
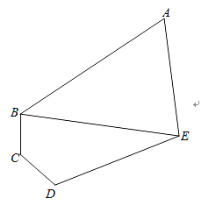
(1)求两区域边界BE的长度;
(2)若区域ABE为锐角三角形,求书架总长度AB+AE的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对某校的100名学生进行不记名问卷调查,内容为一周的课外阅读时长和性别等进行统计,如表:
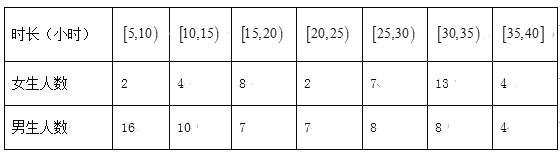
(1)课外阅读时长在20以下的女生按分层抽样的方式随机抽取7人,再从7人中随机抽取2人,求这2人课外阅读时长不低于15的概率;
(2)将课外阅读时长为25以上的学生视为“阅读爱好”者,25以下的学生视为“非阅读爱好”者,根据以上数据完成2×2列联表:
非阅读爱好者 | 阅读爱好者 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.01的前提下,认为学生的“阅读爱好”与性别有关系?
附:![]() ,
,
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本![]() (万元)与年产量
(万元)与年产量![]() (吨)之间的函数关系式可以近似的表示为
(吨)之间的函数关系式可以近似的表示为![]() ,已知此生产线年产量最大为
,已知此生产线年产量最大为![]() 吨.
吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com