
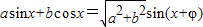 给出公式:
给出公式: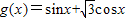 化为:
化为: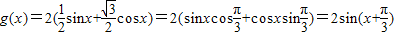
 化为f(x)=Asin(ωx+φ)的形式.
化为f(x)=Asin(ωx+φ)的形式. 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:阅读理解
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
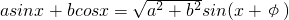 给出公式:
给出公式: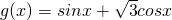 化为:
化为: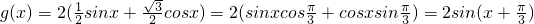
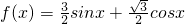 化为f(x)=Asin(ωx+φ)的形式.
化为f(x)=Asin(ωx+φ)的形式.查看答案和解析>>
科目:高中数学 来源:2011年安徽省两地三校高一上学期期末联考数学试卷 题型:解答题
.阅读与理解:
给出公式: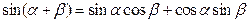 ;
; ;
;
我们可以根据公式将函数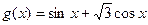 化为:
化为: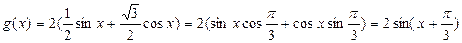
(1)根据你的理解将函数 化为
化为 的形式.
的形式.
(2)求出上题函数 的最小正周期、对称中心.
的最小正周期、对称中心.
(3)求函数在区间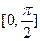 上的最大值、最小值及相应的
上的最大值、最小值及相应的 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:《第1章 三角函数》2013年单元测试卷(4)(解析版) 题型:解答题
 cosx化为:g(x)=2(
cosx化为:g(x)=2( sinx+
sinx+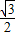 cosx)=2(sinxcos
cosx)=2(sinxcos +cosxsin
+cosxsin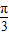 )=2sin(x+
)=2sin(x+ )
) )化为f(x)=Asin(ωx+φ)的形式.
)化为f(x)=Asin(ωx+φ)的形式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com