Question

【题目】设不等式﹣2＜|x﹣1|﹣|x+2|＜0的解集为M，a，b∈M． （Ⅰ）证明：| a+ b|＜ ；
（Ⅱ）比较|1﹣4ab|与2|a﹣b|的大小．

Answer 1

【答案】解：（Ⅰ）记f（x）=|x﹣1|﹣|x+2|= ，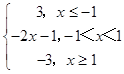

由﹣2＜﹣2x﹣1＜0解得﹣ ＜x＜ ，则M=（﹣ ， ）．

∵a、b∈M，∴|a|＜ ，|b|＜ ，

∴| a+ b|≤ |a|+ |b|＜ ．

（Ⅱ）由（Ⅰ）得a2＜ ，b2＜ ．

因为|1﹣4ab|2﹣4|a﹣b|2=（1﹣8ab+16a2b2）﹣4（a2﹣2ab+b2）

=（4a2﹣1）（4b2﹣1）＞0，…（9分）

所以|1﹣4ab|2＞4|a﹣b|2，故|1﹣4ab|＞2|a﹣b|

【解析】（Ⅰ）利用绝对值不等式的解法求出集合M，利用绝对值三角不等式直接证明；（Ⅱ）利用（Ⅰ）的结果，说明ab的范围，比较|1﹣4ab|与2|a﹣b|两个数的平方差的大小，即可得到结果．