
【题目】在如图所示的空间几何体中,平面![]() 平面
平面![]() ,
,![]() 与
与![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,BE和平面ABC所成的角为
,BE和平面ABC所成的角为![]() ,且点E在平面ABC上的射影落在
,且点E在平面ABC上的射影落在![]() 的平分线上.
的平分线上.

(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,设离心率为
,设离心率为![]() ,且满足
,且满足![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点(0,1)的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2020年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
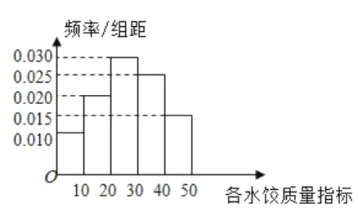
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: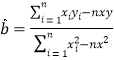 ,
,![]() (精确到
(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在函数定义域内,若存在区间![]() ,使得函数值域为
,使得函数值域为![]() ,则称此函数为“
,则称此函数为“![]() 档类正方形函数”,已知函数
档类正方形函数”,已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 的最大值是1,求实数
的最大值是1,求实数![]() 的值;
的值;
(3)当![]() 时,是否存在
时,是否存在![]() ,使得函数
,使得函数![]() 为“1档类正方形函数”?若存在,求出实数
为“1档类正方形函数”?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,由四个全等的直角三角形和一个正方形构成.现有五种不同的颜色可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( )
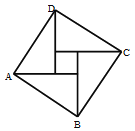
A.180B.192C.420D.480
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com