分析:(1)首先要根据条件变形递推公式得:
=+•,然后通过换元的方法分析得数列
{bn+}是等比数列,其中
=bn.从而可以求得数列{b
n}的通项公式,进而即可求得数列{a
n}的通项公式;
(2)首先要利用基本不等式获得b
2n+b
2n-1•2+…+b
n+1•2
n-1+b
n-1•2
n+1+…+b•2
2n-1+2
2n≥n•2
n+1•b
n,然后对数列{a
n}的通项公式变形然后利用所获得的不等式放缩化简即可获得问题的解答.
解答:解:(1)由题意知:
=,
∴
==+•,
设
=bn,则
bn=bn-1+(n≥2)设
bn+λ=(bn-1+λ),则
bn=bn-1+λ(-1),
当b=2时,
-=,
∴
{}为首项是
,公差是
的等差数列.
∴a
n=2.
当b≠2时,
令
λ(-1) =,∴
λ=,
∴
bn+=(bn-1+) (n≥2),
∴
{bn+}是等比数列.
∴
bn+=(b1+) ()n-1,
又∵
b1=,
∴
bn=()n-=• ,
∴
an=,n∈N*.
综上可知:
当b=2时,a
n=2.
当b≠2时,
an=,n∈N*(2)当b=2时,由(1)知命题显然成立;
当b≠2时,
∵
b2n+22n>2=2n+1•bnb2n-1• 2+ b•22n-1>2=2n+1•bn…
bn+12n-1+bn-12n+1>2=2n+1•bn将以上n个式子相加得:
b
2n+b
2n-1•2+…+b
n+1•2
n-1+b
n-1•2
n+1+…+b•2
2n-1+2
2n>n•2
n+1•b
n∴
an=| n•2n+1•bn•(2-b) |
| 2n+1• (2n-bn) |
<| [(b2n+b2n-1•2+…+b•22n-1+22n)-bn•2n] (b-2) |
| 2n+1•(bn-2n) |
=
| (b2n+b2n-1•2+…+b•22n-1+22n) (b-2) -bn•2n• (b-2) |
| 2n+1•(bn-2n) |
=
| (b2n+1-bn+1•2n)+(bn•2n+1-22n+1) |
| 2n+1•(bn-2n) |
=
+1.
综上可知:
an≤ +1,n∈N*.
点评:本题考查的是数列的递推公式问题.在解答的过程当中充分体现了转化的思想、换元的思想、基本不等式的利用以及放缩法.值得同学们体会和反思.



 阅读快车系列答案
阅读快车系列答案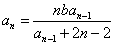 (n≥2)。
(n≥2)。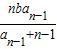 (n≥2)
(n≥2)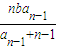 (n≥2)
(n≥2)