
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且cosC= ![]() .
.
(1)求角B的大小;
(2)若BD为AC边上的中线,cosA= ![]() ,BD=
,BD= ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】
(1)解:2bcosC+c=2a,由正弦定理,得2sinBcosC+sinC=2sinA.
∵A+B+C=π,∴sinA=sin(B+C)=sinBcosC+cosBsinC,
∴2sinBcosC+sinC=2(sinBcosC+cosBsinC),∴sinC=2cosBsinC,
∵0<C<π,∴sinC≠0,∴ ![]() .
.
又∵0<B<π,∴B= ![]()
(2)解:在△ABD中,由余弦定理得 ![]() =c2+
=c2+ ![]() ﹣2c×
﹣2c× ![]() cosA,
cosA,
∴ ![]() =c2+
=c2+ ![]() ﹣
﹣ ![]() bc,①,
bc,①,
在△ABC中,由正弦定理得 ![]() =
= ![]() ,由已知得sinA=
,由已知得sinA= ![]() .
.
∴sinC=sin(A+B)=sinAcosB+cosAsinB= ![]() ,
,
∴c= ![]() b…②,
b…②,
由①,②解得b=7,c=5,
∴S△ABC= ![]() bcsinA=10
bcsinA=10 ![]()
【解析】(1)利用正弦定理、和差公式即可得出.(2)在△ABD中,由余弦定理得 ![]() =c2+
=c2+ ![]() ﹣2c×
﹣2c× ![]() cosA,在△ABC中,由正弦定理得
cosA,在△ABC中,由正弦定理得 ![]() =
= ![]() ,由已知得sinA=
,由已知得sinA= ![]() .再利用sinC=sin(A+B)=sinAcosB+cosAsinB=
.再利用sinC=sin(A+B)=sinAcosB+cosAsinB= ![]() ,联立解出.
,联立解出.
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】过点(0,4),斜率为﹣1的直线与抛物线y2=2px(p>0)交于两点A、B,且弦|AB|的长度为4![]() .
.
(1)求p的值;
(2)求证:OA⊥OB(O为原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾天气对城市环境造成很大影响,按照国家环保部发布的标准:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米.某市环保部门加强了对空气质量的监测,抽取某居民区监测点的20天PM2.5的24小时平均浓度的监测数据,制成茎叶图,如图:
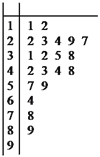
(Ⅰ)完成如下频率分布表,并在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
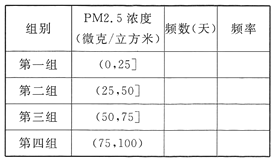
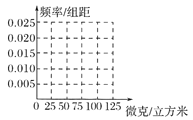
(Ⅱ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在区间[﹣1,1]上任取两个数a,b,在下列条件时,分别求不等式x2+2ax+b2≥0恒成立时的概率:
(1)当a,b均为整数时;
(2)当a,b均为实数时.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位招聘职工分为笔试和面试两个环节,将笔试成绩合格(满分100分,及格60分,精确到个位数)的应聘者进行统计,得到如下的频率分布表:
分组 | 频数 | 频率 |
[60,70] |
| 0.16 |
(70,80] | 22 |
|
(80,90] | 14 | 0.28 |
(90,100] |
|
|
合计 | 50 | 1 |
(Ⅰ)确定表中![]() 的值(直接写出结果,不必写过程)
的值(直接写出结果,不必写过程)
(Ⅱ)面试规定,笔试成绩在80分(不含80分)以上者可以进入面试环节,面试时又要分两关,首先面试官依次提出4个问题供选手回答,并规定,答对2道题就终止回答,通过第一关可以进入下一关,如果前三题均没有答对,则不再回答第四题并且不能进入下一关,假定某选手获得面试资格的概率与答对每道题的概率相等.
![]() 求该选手答完3道题而通过第一关的概率;
求该选手答完3道题而通过第一关的概率;
![]() 记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)= ![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①f(﹣x)+f(x)=0在x∈R时恒成立;
②函数f(x)的值域为(﹣1,1);
③若x1≠x2 , 则一定有f(x1)≠f(x2);
④函数g(x)=f(x)﹣x在R上有三个零点.
其中正确结论的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为: ![]() =1(a>0),其焦点在x轴上,离心率e=
=1(a>0),其焦点在x轴上,离心率e= ![]() .
.
(1)求该椭圆的标准方程;
(2)设动点P(x0 , y0)满足 ![]() ,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣
,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣ ![]() ,求证:x02+2y02为定值.
,求证:x02+2y02为定值.
(3)在(2)的条件下,问:是否存在两个定点A,B,使得|PA|+|PB|为定值?若存在,给出证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图 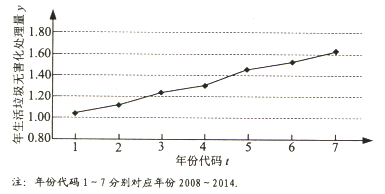
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据: ![]() =9.32,
=9.32, ![]() yi=40.17,
yi=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:相关系数r= 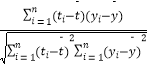 回归方程
回归方程 ![]() =
= ![]() +
+ ![]() t 中斜率和截距的最小二乘估计公式分别为:
t 中斜率和截距的最小二乘估计公式分别为: ![]() =
= 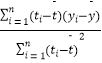 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,且,
,且, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() ,且
,且![]() 为
为![]() 的中点.
的中点.
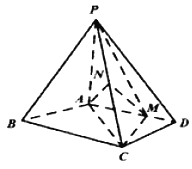
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com