
【题目】已知函数f(x)=ln(ax+1)+ ![]() ﹣x2﹣ax(a∈R)
﹣x2﹣ax(a∈R)
(1)若y=f(x)在[4,+∞)上为增函数,求实数a的取值范围;
(2)当a≥ ![]() 时,设g(x)=ln[x2(ax+1)]+
时,设g(x)=ln[x2(ax+1)]+ ![]() ﹣3ax﹣f(x)(x>0)的两个极值点x1 , x2(x1<x2)恰为φ(x)=lnx﹣cx2﹣bx的零点,求y=(x1﹣x2)φ′(
﹣3ax﹣f(x)(x>0)的两个极值点x1 , x2(x1<x2)恰为φ(x)=lnx﹣cx2﹣bx的零点,求y=(x1﹣x2)φ′( ![]() )的最小值.
)的最小值.
【答案】
(1)解:由题意f′(x)= ![]() +x2﹣2x﹣a≥0在[4,+∞)上恒成立,
+x2﹣2x﹣a≥0在[4,+∞)上恒成立,
整理得ax2+(1﹣2a)x﹣a2﹣2≥0在[4,+∞)上恒成立
设h(x)=ax2+(1﹣2a)x﹣a2﹣2,显然a>0其对称轴为x=1﹣ ![]() <1
<1
∴h(x)在[4,+∞)单调递增,∴只要h(4)=16a+4(1﹣2a)﹣a2﹣2≥0,
∴0<a≤4+3 ![]()
(2)解:g(x)=2lnx﹣2ax+x2,g′(x)= ![]() .
.
由题意  ,∴
,∴ ![]() ≥
≥ ![]() ,解得0<
,解得0< ![]() ≤
≤ ![]() ,
,
φ′(x)= ![]() ﹣2cx﹣b,φ(x1)=lnx1﹣cx12﹣bx1,φ(x2)=lnx2﹣cx22﹣bx2,
﹣2cx﹣b,φ(x1)=lnx1﹣cx12﹣bx1,φ(x2)=lnx2﹣cx22﹣bx2,
两式相减得ln ![]() ﹣c(x1﹣x2)(x1+x2)﹣b(x1﹣x2)=0,
﹣c(x1﹣x2)(x1+x2)﹣b(x1﹣x2)=0,
∴y=(x1﹣x2)φ′( ![]() )=
)= ![]() ﹣lnt(0<t≤
﹣lnt(0<t≤ ![]() ),
),
∴y′= ![]() <0.
<0.
∴y=(x1﹣x2)φ′( ![]() )在(0,
)在(0, ![]() ]递减,ymin=ln2﹣
]递减,ymin=ln2﹣ ![]() .
.
∴y=(x1﹣x2)φ′( ![]() )的最小值为ln2﹣
)的最小值为ln2﹣ ![]()
【解析】(1)由题意f′(x)= ![]() +x2﹣2x﹣a≥0在[4,+∞)上恒成立,整理得ax2+(1﹣2a)x﹣a2﹣2≥0在[4,+∞)上恒成立,设h(x)=ax2+(1﹣2a)x﹣a2﹣2,只要h(4)=16a+4(1﹣2a)﹣a2﹣2≥0,即可求实数a的取值范围;(2)先确定0<
+x2﹣2x﹣a≥0在[4,+∞)上恒成立,整理得ax2+(1﹣2a)x﹣a2﹣2≥0在[4,+∞)上恒成立,设h(x)=ax2+(1﹣2a)x﹣a2﹣2,只要h(4)=16a+4(1﹣2a)﹣a2﹣2≥0,即可求实数a的取值范围;(2)先确定0< ![]() ≤
≤ ![]() ,再利用y=(x1﹣x2)φ′(
,再利用y=(x1﹣x2)φ′( ![]() )=
)= ![]() ﹣lnt(0<t≤
﹣lnt(0<t≤ ![]() ),即可求y=(x1﹣x2)φ′(
),即可求y=(x1﹣x2)φ′( ![]() )的最小值.
)的最小值.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
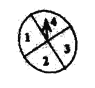
【题目】在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯![]() 关时,转
关时,转![]() 次,当次转得数字之和大于
次,当次转得数字之和大于![]() 时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍,假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.
时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍,假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.
(1)求某人参加一次游戏,恰好获得10欧元的概率;
(2)某人参加一次游戏,获得奖金![]() 欧元,求
欧元,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2≥a;命题q:x∈R,x2+2ax+2﹣a=0,若命题p∧q是真命题,则实数a的取值范围是( )
A.a≤﹣2或a=1
B.a≤﹣2或1≤a≤2
C.a≥1
D.﹣2≤a≤1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)(x≠0)对于任意的x,y∈R且x,y≠0满足f(xy)=f(x)+f(y).
(1)求f(1),f(﹣1)的值;
(2)求证:y=f(x)为偶函数;
(3)若y=f(x)在(0,+∞)上是增函数,解不等式 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x+1|<1},B={x|y= ![]() ,y∈R},则A∩RB=( )
,y∈R},则A∩RB=( )
A.(﹣2,1)
B.(﹣2,﹣1]
C.(﹣1,0)
D.[﹣1,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com