
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
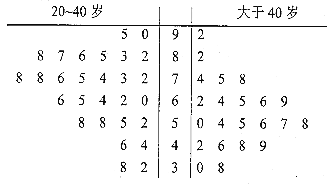
(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,记抽到的2人中年龄大于40岁的市民人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.

【答案】(Ⅰ)表格如解析所示,没有95%的把握认为市民是否购买该款手机与年龄有关;(Ⅱ)X的分布列如解析所示,期望为![]() .
.
【解析】
试题分析:(Ⅰ)根据茎叶图可填表格,再由公式计算![]() ,并且和
,并且和![]() 比较大小,即可得出结论;(Ⅱ)根据层比为
比较大小,即可得出结论;(Ⅱ)根据层比为![]() ,分别得到年龄在20~40岁的抽取了2人,年龄大于40岁的抽取了3人,分别对这
,分别得到年龄在20~40岁的抽取了2人,年龄大于40岁的抽取了3人,分别对这![]() 人分类标号,并通过列举法计算出所有可能出现的情况,即可求出X的分布列和期望值.
人分类标号,并通过列举法计算出所有可能出现的情况,即可求出X的分布列和期望值.
试题解析:(Ⅰ)由茎叶图可得:
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | 20 | 8 | 28 |
大于40岁 | 10 | 12 | 22 |
合计 | 30 | 20 | 50 |
由列联表可得:![]() ,
,
所以,没有95%的把握认为市民是否购买该款手机与年龄有关.
(Ⅱ)购买意愿弱的市民共有20人,抽样比例为![]() ,
,
所以年龄在20~40岁的抽取了2人,年龄大于40岁的抽取了3人,
则X的可能取值为0,1,2,
![]() ,
,
所以分布列为
X | 0 | 1 | 2 |
P |
|
|
|
数学期望为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,![]() 获得本场比赛胜利,最终人机大战总比分定格在
获得本场比赛胜利,最终人机大战总比分定格在![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
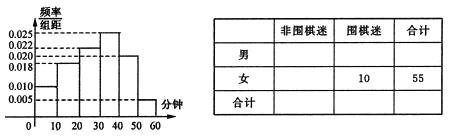
(1)根据已知条件完成如图列联表,并据此资料判断你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.010 |
| 3.74 | 6.63 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,其左、右顶点为
,其左、右顶点为![]() 、
、![]() ,椭圆与
,椭圆与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,
,![]() 的外接圆的圆心
的外接圆的圆心![]() 在直线
在直线![]() 上.
上.
(I)求椭圆![]() 的方程;
的方程;
(II)已知直线![]() :
:![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() ,垂足为
,垂足为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,专家发现,学生的注意力着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f(t)表示学生注意力随时间t(分钟)的变化规律\left(f(t)越大,表明学生注意力越集中),经过实验分析得知: 
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,教师能否在学生达到所需的状态下讲授完这道题目?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强环保意识,某社团从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(2)为参加市举办的环保知识竞赛,学校举办预选赛,现在环保测试优秀的同学中选3人参加预选赛,已知在环保测试中优秀的同学通过预选赛的概率为![]() ,若随机变量
,若随机变量![]() 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:![]() =
=![]()
| 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=![]() .
.
(1)求证:C1B⊥平面ABC;
设![]() (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
试求λ的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com