
【题目】设P为双曲线![]() 上任一点,
上任一点,![]() ,则以
,则以![]() 为直径的圆与以双曲线实轴长为直径的圆( )
为直径的圆与以双曲线实轴长为直径的圆( )
A.相切B.相交C.相离D.内含
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 是等边三角形,且平面
是等边三角形,且平面![]()
![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
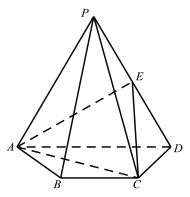
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲和乙两个人计划周末参加志愿者活动,约定在周日早上8:00至8:30之间到某公交站搭乘公交车一起去,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为8:05,8:15,8:30,如果他们约定见车就搭乘,则甲和乙两个人恰好能搭乘同一班公交车去的概率为( )
班公交车到达该站,到站的时间分别为8:05,8:15,8:30,如果他们约定见车就搭乘,则甲和乙两个人恰好能搭乘同一班公交车去的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,且
上的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)若![]() 是椭圆
是椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冬天的北方室外温度极低,若轻薄保暖的石墨烯发热膜能用在衣服上,可爱的医务工作者行动会更方便.石墨烯发热膜的制作:从石墨中分离出石墨烯,制成石墨烯发热膜.从石墨分离石墨烯的一种方法是化学气相沉积法,使石墨升华后附着在材料上再结晶.现在有![]() 材料、
材料、![]() 材料供选择,研究人员对附着在
材料供选择,研究人员对附着在![]() 材料、
材料、![]() 材料上再结晶各做了50次试验,得到如下等高条形图.
材料上再结晶各做了50次试验,得到如下等高条形图.
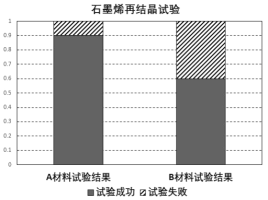
(1)根据上面的等高条形图,填写如下列联表,判断是否有99%的把握认为试验成功与材料有关?
|
| 合计 | |
成功 | |||
不成功 | |||
合计 |
(2)研究人员得到石墨烯后,再制作石墨烯发热膜有三个环节:①透明基底及![]() 胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为
胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为![]() ,第三个环节生产合格的概率为
,第三个环节生产合格的概率为![]() ,且各生产环节相互独立.已知生产1吨的石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三个环节的修复费用为3000元,其余环节修复费用均为1000元.如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标?
,且各生产环节相互独立.已知生产1吨的石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三个环节的修复费用为3000元,其余环节修复费用均为1000元.如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标?
附:参考公式: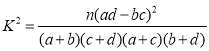 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,离心率为
,离心率为![]() ,双曲线
,双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,已知
,已知![]() ,
,![]() .
.
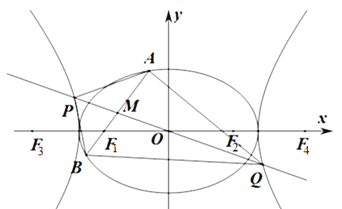
(1)求![]() ,
,![]() 的方程;
的方程;
(2)过![]() 作
作![]() 的不垂直于
的不垂直于![]() 轴的弦
轴的弦![]() ,
,![]() 为弦
为弦![]() 的中点,当直线
的中点,当直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点时,求四边形
两点时,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,若{bn}的前n项和为Tn,证明:Tn<
,若{bn}的前n项和为Tn,证明:Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com