
 如图是将二进制数11111(2)化为十进制数的一个程序框图.
如图是将二进制数11111(2)化为十进制数的一个程序框图.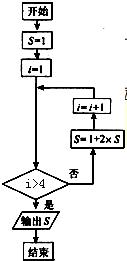 解:(1)首先将二进制数11111(2)化为十进制数,
解:(1)首先将二进制数11111(2)化为十进制数,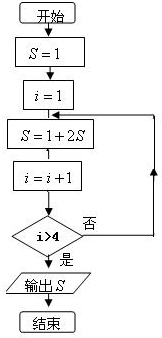 用直到型循环结构改写流程图,如图所示.
用直到型循环结构改写流程图,如图所示.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:2014届黑龙江省高二上学期期末理科数学试卷(解析版) 题型:选择题
如图是将二进制数11111(2)化为十进制数的一个程序框图,判断框内应填入的条件是( )

A.i≤5 B.i≤4 C.i>5 D.i>4
查看答案和解析>>
科目:高中数学 来源:2013届湖北省武汉市高二上学期期中数学试卷(解析版) 题型:选择题
如图是将二进制数11111(2)化为十进制数的一个程序框图,判断框内应填入的条件是

A.i≤5 B.i≤4 C.i>5 D.i>4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com