
【题目】设递增等比数列{an}的前n项和为Sn,且a2=3,S3=13,数列{bn}满足b1=a1,点P(bn,bn+1)在直线x﹣y+2=0上,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)设cn![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
【答案】(1)an=3n﹣1,bn=2n﹣1(2)Tn=3﹣(n+1)(![]() )n﹣1
)n﹣1
【解析】
(1)利用基本量法求解![]() ,再代入
,再代入![]() 到直线
到直线![]() 可得
可得![]() 为等差数列,再进行通项公式求解即可.
为等差数列,再进行通项公式求解即可.
(2)利用错位相减求和即可.
(1)递增等比数列{an}的公比设为q,前n项和为Sn,且a2=3,S3=13,
可得a1q=3,a1+a1q+a1q2=13,解得q=3或q![]() ,
,
由等比数列递增,可得q=3,a1=1,则![]() ;
;
P(bn,bn+1)在直线x﹣y+2=0上,可得bn+1﹣bn=2,
且b1=a1=1,则bn=1+2(n﹣1)=2n﹣1;
(2)cn![]() (2n﹣1)(
(2n﹣1)(![]() )n﹣1,
)n﹣1,
前n项和Tn=11+3![]() 5
5![]() (2n﹣1)(
(2n﹣1)(![]() )n﹣1,
)n﹣1,
![]() Tn=1
Tn=1![]() 3
3![]() 5
5![]() (2n﹣1)(
(2n﹣1)(![]() )n,
)n,
相减可得![]() Tn=1+2(
Tn=1+2(![]() (
(![]() )n﹣1)﹣(2n﹣1)(
)n﹣1)﹣(2n﹣1)(![]() )n
)n
=1+2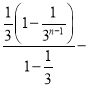 (2n﹣1)(
(2n﹣1)(![]() )n,
)n,
化简可得Tn=3﹣(n+1)(![]() )n﹣1.
)n﹣1.


科目:高中数学 来源: 题型:
【题目】在平面坐标系中xOy中,已知直线l的参数方程为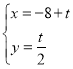 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为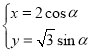 (
(![]() 为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
(1)求曲线C的普通方程和直线l的极坐标方程;
(2)设P为曲线C上的动点,求点P到直线l的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解居民的用电情况,某地供电局抽查了该市若干户居民月均用电量(单位:![]() ),并将样本数据分组为
),并将样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示.
,其频率分布直方图如图所示.
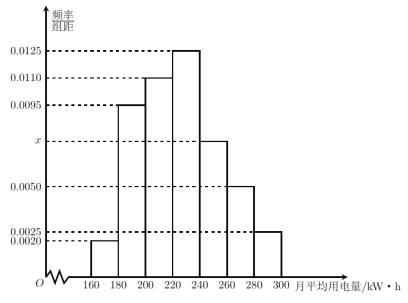
(1)若样本中月均用电量在![]() 的居民有
的居民有![]() 户,求样本容量;
户,求样本容量;
(2)求月均用电量的中位数;
(3)在月均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组居民中,用分层随机抽样法抽取
的四组居民中,用分层随机抽样法抽取![]() 户居民,则月均用电量在
户居民,则月均用电量在![]() 的居民应抽取多少户?
的居民应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面是边长为2的正方形,平面PAD⊥平面ABCD,PA⊥AD,∠PDA=45°,E,F分别为AB,PC的中点.
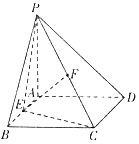
(1)证明:EF∥平面PAD;
(2)在线段BC上是否存在一点H,使平面PAH⊥平面DEF?若存在,求此时二面角C﹣HD﹣P的平面角的正切值:若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
某产品按行业生产标准分成8个等级,等级系数X依次为1,2,……,8,其中X≥5为标准A,X≥3为标准B,已知甲厂执行标准A生产该产品,产品的零售价为6元/件;乙厂执行标准B生产该产品,产品的零售价为4元/件,假定甲、乙两厂得产品都符合相应的执行标准
(I)已知甲厂产品的等级系数X1的概率分布列如下所示:

且X1的数字期望EX1=6,求a,b的值;
(II)为分析乙厂产品的等级系数X2,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数X2的数学期望.
![]() 在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
注:(1)产品的“性价比”=![]() ;
;
(2)“性价比”大的产品更具可购买性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为椭圆
为椭圆![]() 的左右焦点,
的左右焦点,![]() 在以
在以![]() 为圆心,1为半径的圆
为圆心,1为半径的圆![]() 上,且
上,且![]() .
.
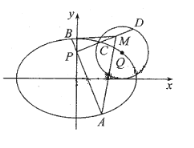
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 与
与![]() 垂直的直线
垂直的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线y2=4x的焦点相同,F1,F2为C的左右焦点,M为C上任意一点,
的一个焦点与抛物线y2=4x的焦点相同,F1,F2为C的左右焦点,M为C上任意一点,![]() 最大值为1.
最大值为1.
(1)求椭圆C的方程;
(2)不过点F2的直线l:y=kx+m(m≠0)交椭圆C于A,B两点.
①若![]() ,且
,且![]() ,求m的值.
,求m的值.
②若x轴上任意一点到直线AF2与BF2距离相等,求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com