
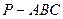 中,
中,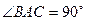 ,
,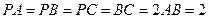 ,
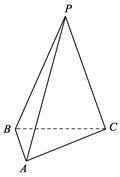
,
 面
面
 的余弦值.
的余弦值. 为直角三角形,
为直角三角形,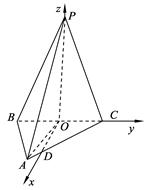
 POA=∠POB=∠POC=90°,∴PO⊥OB,PO⊥OA,OB∩OA=O
POA=∠POB=∠POC=90°,∴PO⊥OB,PO⊥OA,OB∩OA=O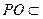 面ABC,∴面PBC⊥面ABC………………………5分
面ABC,∴面PBC⊥面ABC………………………5分
|
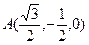 ,
,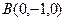 ,
, ,
,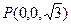 ,
,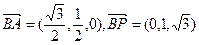 …………………7分
…………………7分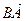 =0,n1·
=0,n1·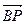 =0,可知n1=(1,-
=0,可知n1=(1,-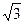 ,1)
,1) 理可求得面PAC的法
理可求得面PAC的法 向量为n1=(3,
向量为n1=(3,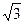 ,1)…………………………………10分
,1)…………………………………10分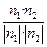 =
=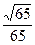 ……………………………………………………12分
……………………………………………………12分

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源:不详 题型:单选题
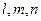 是三条不重合的直线,
是三条不重合的直线, 是三个不重合的平面,给出下列四个命题:
是三个不重合的平面,给出下列四个命题:
 与平面
与平面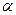 所成的角相等,则
所成的角相等,则 //
// ;
; ,使得
,使得 //
//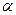 ,
, //
//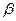 ,
, //
//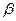 ,则
,则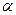 //
//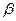 ;
; ,则
,则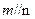 ;
;| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com