Question

【题目】如图，某种水箱用的“浮球”，是由两个半球和一个圆柱筒组成的．已知半球的直径是6 cm，圆柱筒高为2 cm.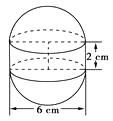

（1）这种“浮球”的体积是多少cm3（结果精确到0.1）?
（2）要在2 500个这样的“浮球”表面涂一层胶，如果每平方米需要涂胶100克，那么共需胶多少克？

Answer 1

【答案】
（1）解：因为半球的直径是6 cm，所以半径R＝3 cm，
所以两个半球的体积之和为V球＝ πR3＝ π·27＝36π（cm3）．
又圆柱筒的体积为V圆柱＝πR2·h＝π×9×2＝18π（cm3）．
所以这种“浮球”的体积是V＝V球＋V圆柱＝36π＋18π＝54π≈169.6（cm3）
（2）解：上下两个半球的表面积是S球表＝4πR2＝4×π×9＝36π（cm2），
又“浮球”的圆柱筒的侧面积为S圆柱侧＝2πRh＝2×π×3×2＝12π（cm2），
所以1个“浮球”的表面积为S＝ ＝ π（m2）．
因此2 500个这样的“浮球”的表面积为2 500S＝2 500× π＝12π（m2）．
因为每平方米需要涂胶100克，所以共需要胶的质量为100×12π＝1200π（克）
【解析】(1)浮球由两个半球和一个圆柱筒组成的,由球的体积公式及圆柱的体积公式求得其体积;
(2)“浮球”表面涂一层胶即就是要求其表面积,由表面活性剂积决定涂胶克数.
【考点精析】本题主要考查了旋转体（圆柱、圆锥、圆台）的相关知识点，需要掌握常见的旋转体有：圆柱、圆锥、圆台、球才能正确解答此题．