
【题目】已知正方形![]() 边长为
边长为![]() ,
,![]() 若在正方形边上恰有
若在正方形边上恰有![]() 个不同的点
个不同的点![]() ,使
,使![]() ,则
,则![]() 的取值范围为_____________.
的取值范围为_____________.
【答案】![]()
【解析】
建立坐标系,逐段分析![]()
![]() 的取值范围及对应的解得答案.
的取值范围及对应的解得答案.
以AB所在直线为x轴,以AD所在直线为y轴建立平面直角坐标系如图:

则F(0,2),E(8,4)
(1)若P在AB上,设P(x,0),0≤x≤8
∴![]() (﹣x,2),
(﹣x,2),![]() (8﹣x,4)
(8﹣x,4)
∴![]()
![]() x2﹣8x+8,
x2﹣8x+8,
∵x∈[0,8],∴﹣8![]()
![]() 8,
8,
∴当λ=﹣8时有一解,当﹣8<λ≤8时有两解;
(2)若P在AD上,设P(0,y),0<y≤8,
∴![]() (0,2﹣y),
(0,2﹣y),![]() (8,4﹣y)
(8,4﹣y)
∴![]()
![]() (2﹣y)(4﹣y)=y2﹣6y+8
(2﹣y)(4﹣y)=y2﹣6y+8
∵0<y≤8,∴﹣1![]()
![]() 24
24
∴当λ=﹣1或8<λ<24时有唯一解;当﹣1<λ≤8时有两解
(3)若P在DC上,设P(x,8),0<x≤8
∴![]() (﹣x,﹣6),
(﹣x,﹣6),![]() (8﹣x,﹣4),
(8﹣x,﹣4),
∴![]()
![]() x2﹣8x+24,
x2﹣8x+24,
∵0<x≤8,∴8![]()
![]() 24,
24,
∴当λ=8时有一解,当8<λ≤24时有两解.
(4)若P在BC上,设P(8,y),0<y<8,
∴![]() (﹣8,2﹣y),
(﹣8,2﹣y),![]() (0,4﹣y),
(0,4﹣y),
∴![]()
![]() (2﹣y)(4﹣y)=y2﹣6y+8
(2﹣y)(4﹣y)=y2﹣6y+8
∵0<y<8,∴﹣1![]()
![]() 24,
24,
∴当λ=﹣1或8<λ<24时有一解,当﹣1<λ≤8时有两解.
综上,在正方形ABCD的四条边上有且只有6个不同的点P,使得![]()
![]() λ成立,那么λ的取值范围是(﹣1,8)
λ成立,那么λ的取值范围是(﹣1,8)
故答案为:(﹣1,8)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数 ,回归直线方程
,回归直线方程![]() ,
,
其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中正确的是( )
A.空间的任何一个向量都可用其他三个向量表示
B.若![]() 为空间向量的一组基底,则
为空间向量的一组基底,则![]() 构成空间向量的另一组基底
构成空间向量的另一组基底
C.![]() 为直角三角形的充要条件是
为直角三角形的充要条件是![]()
D.任何三个不共线的向量都可构成空间向量的一个基底
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下5条表述中,横线上填A代表“充分非必要条件”,填B代表“必要非充分条件”,填C代表“充要条件”,填D代表“既非充分也非必要条件”,请将相应的字母填入下列横线上.
(1)若![]() ,则“
,则“![]() 是
是![]() 与
与![]() 的等比中项”是“
的等比中项”是“![]() ”的_______.
”的_______.
(2)“数列![]() 为常数列”是“数列
为常数列”是“数列![]() 既是等差数列又是等比数列”的_______.
既是等差数列又是等比数列”的_______.
(3)若![]() 是等比数列,则“
是等比数列,则“![]() ”是“
”是“![]() 为递减数列”的_______.
为递减数列”的_______.
(4)若![]() 是公比为
是公比为![]() 的等比数列,则“
的等比数列,则“![]() ”是“
”是“![]() 是递减数列”的_______.
是递减数列”的_______.
(5)记数列![]() 的前
的前![]() 项和为
项和为![]() ,则“数列
,则“数列![]() 为递增数列”是“数列
为递增数列”是“数列![]() 的各项均为大于零”的_______.
的各项均为大于零”的_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国神舟十一号载人飞船在酒泉卫星发射中心成功发射,引起全国轰动.开学后,某校高二年级班主任对该班进行了一次调查,发现全班60名同学中,对此事关注的占![]() ,他们在本学期期末考试中的物理成绩(满分100分)如下面的频率分布直方图:
,他们在本学期期末考试中的物理成绩(满分100分)如下面的频率分布直方图:

(1)求“对此事关注”的同学的物理期末平均分(以各区间的中点代表该区间的均值).
(2)若物理成绩不低于80分的为优秀,请以是否优秀为分类变量,
①补充下面的![]() 列联表:
列联表:
物理成绩优秀 | 物理成绩不优秀 | 合计 | |
对此事关注 | |||
对此事不关注 | |||
合计 |
②是否有![]() 以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系?
以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系?
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量.2007年至2018年,某企业连续12年累计研发投入达4100亿元,我们将研发投入与经营收入的比值记为研发投入占营收比.这12年间的研发投入(单位:十亿元)用图中的条形图表示,研发投入占营收比用图中的折线图表示.

根据折线图和条形图,下列结论错误的是( )
A. 2012﹣2013 年研发投入占营收比增量相比 2017﹣2018 年增量大
B. 该企业连续 12 年研发投入逐年增加
C. 2015﹣2016 年研发投入增值最大
D. 该企业连续 12 年研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式。孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数p,使得p+2是素数,素数对(p,p+2)称为孪生素数.在不超过30的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.
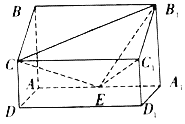
(1)证明:![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com