
| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
分析 可设g(x)=$\frac{f(x)}{x}$,根据条件可以判断g(x)为偶函数,并可得到x>0时,g′(x)<0,从而得出g(x)在(0,+∞)上单调递减,并且g(2)=0,从而由g(x)>g(2)便可得到|x|<2,且x≠0,这样即可得出原不等式的解集.
解答 解:设g(x)=$\frac{f(x)}{x}$,f(x)是R上的奇函数,∴g(x)为偶函数;
x>0时,$g′(x)=\frac{xf′(x)-f(x)}{{x}^{2}}<0$;
∴g(x)在(0,+∞)上单调递减,g(2)=0;
∴由g(x)>0得,g(x)>g(2);
∴g(|x|)>g(2);
∴|x|<2,且x≠0;
∴-2<x<0,或0<x<2;
∴$\frac{f(x)}{x}>0$的解集为(-2,0)∪(0,2).
故选:B.
点评 考查奇函数、偶函数的定义,根据导数符号判断函数单调性的方法,根据函数单调性解不等式的方法,知道偶函数g(x)>g(2)等价于g(|x|)>g(2).


科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(理)试卷(解析版) 题型:选择题
设集合P={x∈R|x2+2x<0},Q={x∈R| 1/(x+1)>0},则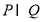 =( )
=( )
A.(﹣2,1) B.(﹣1,0) C.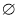 D.(﹣2,0)
D.(﹣2,0)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com