
(本题满分13分) 如图, 是离心率为
是离心率为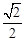 的椭圆,
的椭圆,
 :
: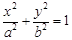 (
(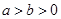 )的左、右焦点,直线
)的左、右焦点,直线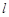 :
: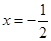 将线段
将线段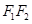 分成两段,其长度之比为1 : 3.设
分成两段,其长度之比为1 : 3.设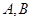 是
是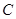 上的两个动点,线段
上的两个动点,线段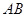 的中点
的中点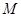 在直线
在直线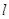 上,线段
上,线段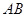 的中垂线与
的中垂线与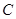 交于
交于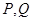 两点.
两点.

(Ⅰ) 求椭圆C的方程;
(Ⅱ) 是否存在点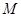 ,使以
,使以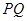 为直径的圆经过点
为直径的圆经过点 ,若存在,求出
,若存在,求出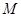 点坐标,若不存在,请说明理由.
点坐标,若不存在,请说明理由.
(Ⅰ)  (Ⅱ) 存在两点
(Ⅱ) 存在两点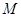 符合条件,坐标为
符合条件,坐标为 ,理由见解析
,理由见解析
【解析】
试题分析:(Ⅰ) 设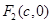 ,则
,则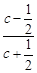 =
=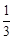 ,所以
,所以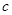 =1.
=1.
因为离心率e=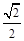 ,所以
,所以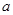 =
=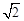 .
.
所以椭圆C的方程为 .
……5分
.
……5分
(Ⅱ) 当直线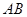 垂直于
垂直于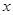 轴时,直线
轴时,直线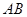 方程为
方程为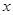 =-
=-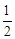 ,
,
此时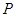 (
(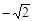 ,0)、
,0)、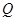 (
(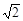 ,0)
,
,0)
,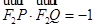 .不合题意;
……7分
.不合题意;
……7分
当直线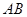 不垂直于
不垂直于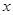 轴时,设存在点
轴时,设存在点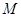 (-
(-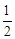 ,
,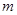 ) (
) (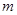 ≠0),直线
≠0),直线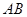 的斜率为
的斜率为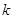 ,
,
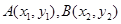 .
.
由 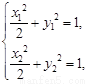 得
得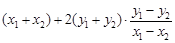 =0,则
=0,则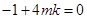 ,
,
故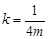 .此时,直线
.此时,直线 斜率为
斜率为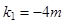 ,
,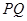 的直线方程为
的直线方程为 .
.
即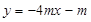 .
.
联立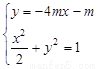 消去
消去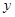 ,整理得
,整理得 .
.
所以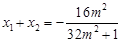 ,
, .
……10分
.
……10分
由题意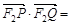 0,于是
0,于是
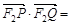
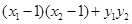
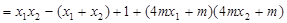
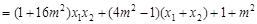

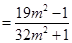 =0.
=0.
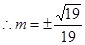
因为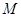 在椭圆内,
在椭圆内,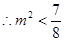
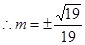 符合条件;
符合条件;
综上,存在两点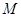 符合条件,坐标为
符合条件,坐标为 .
……13分
.
……13分
考点:本小题主要考查椭圆标准方程的求法和直线与椭圆位置关系的判断和应用以及向量数量积的应用,考查学生分析问题、解决问题的能力和运算求解能力.
点评:设直线方程时,要考虑到直线方程斜率是否存在;对于探究性问题,可以先假设存在,再进行计算,如果能求出来,就说明存在,如果求不出来或者得出矛盾,则说明不存在.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源:2012届浙江省宁波万里国际学校高三上期中理科数学试卷(解析版) 题型:解答题
(本题满分13分) 的三个内角
的三个内角 依次成等差数列.
依次成等差数列.
(Ⅰ)若 ,试判断
,试判断 的形状;
的形状;
(Ⅱ)若 为钝角三角形,且
为钝角三角形,且 ,求
,求
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市朝阳区高三上学期期末考试理科数学 题型:解答题
(本题满分13分)
在锐角 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,且
,且 ,
, ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三上学期期末考试数学理卷(一级学校) 题型:解答题
(本题满分13分)
如图,在五面体ABCDEF中,FA 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD,AF=AB=BC=FE=
AD,AF=AB=BC=FE= AD.
AD.
(Ⅰ)求异面直线BF与DE所成角的余弦值;
(Ⅱ)在线段CE上是否存在点M,使得直线AM与平面CDE所成角的正弦值为 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com