练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在正四棱锥P－ABCD中，PA＝AB，M是BC的中点，G是△PAD的重心，则在平面PAD中经过G点且与直线PM垂直的直线有　　　　条.

    设正四棱锥的底面边长为a，

    则侧棱长为a.

    由PM⊥BC，

    ∴PM＝＝a.

    连接PG并延长与AD相交于N点，

    则PN＝a，MN＝AB＝a，

    ∴PM2＋PN2＝MN2，

    ∴PM⊥PN，又PM⊥AD，

    ∴PM⊥平面PAD，

    ∴在平面PAD中经过G点的任意一条直线都与PM垂直.

    答案：无数

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高中数学综合题 题型：022

    正四棱锥P－ABC的五个顶点在同一球面上， 若正四棱锥的底面边长为4，侧棱长为2，则此球的表面积为________．

    查看答案和解析>>

    科目：高中数学 来源：安徽省蚌埠二中2011－2012学年高二上学期期中考试数学文科试题 题型：013

    在正三棱锥P－ABC中，D、E分别是AB、BC的中点，有下列四个论断：

    ①AC⊥PB；

    ②AC∥平面PDE；

    ③AB⊥平面PDE；

    ④平面PDE⊥平面ABC．其中正确的个数为

    [　　]
    A．

    1个

    B．

    2个

    C．

    3个

    D．

    4个

    查看答案和解析>>

    科目：高中数学 来源：导学大课堂选修数学2-1苏教版 苏教版 题型：013

    如图，在正三棱锥P－ABC中，D是侧棱PA的中点，O是底面ABC的中心，则下列四个结论中正确的是

    [　　]
    A．

    OD∥平面PBC

    B．

    OD⊥PA

    C．

    OD⊥AC

    D．

    PA＝2OD

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，在正三棱锥P－ABC中，D是侧棱PA的中点，O是底面ABC的中心，则下列四个结论中正确的是（      ）

    A、OA∥平面PBC  B、OD⊥PA   C、OD⊥AC    D、PA=2OD

    查看答案和解析>>

    科目：高中数学 来源： 题型：

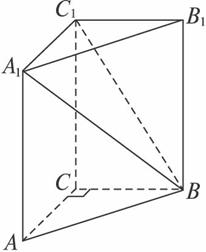
    (理)如图4,在体积为1的直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=1.求直线A1B与平面BB1C1C所成角的大小(结果用反三角函数值表示).

    图4

    (文)如图5,在正四棱锥P—ABCD中,PA=2,直线PA与平面ABCD所成的角为60°,求正四棱锥P—ABCD的体积V.

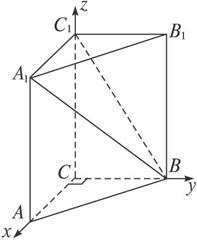
    图5

    查看答案和解析>>

    同步练习册答案