
【题目】给出以下关于线性方程组解的个数的命题.
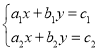 ①,
①,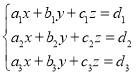 ②,
②,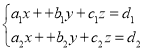 ③,
③, ④,
④,
(1)方程组①可能有无穷多组解;
(2)方程组②可能有且只有两组不同的解;
(3)方程组③可能有且只有唯一一组解;
(4)方程组④可能有且只有唯一一组解.
其中真命题的序号为________________.
科目:高中数学 来源: 题型:
【题目】某投资公司计划在甲、乙两个互联网创新项目上共投资1200万元,每个项目至少要投资300万元.根据市场分析预测:甲项目的收益![]() 与投入
与投入![]() 满足
满足![]() ,乙项目的收益
,乙项目的收益![]() 与投入
与投入![]() 满足
满足![]() .设甲项目的投入为
.设甲项目的投入为![]() .
.
(1)求两个项目的总收益关于![]() 的函数
的函数![]() .
.
(2)如何安排甲、乙两个项目的投资,才能使总收益最大?最大总收益为多少?(注:收益与投入的单位都为“万元”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车包括纯电动汽车、增程式电动汽车、混合动力汽车、燃料电池电动汽车、氢发动机汽车、其他新能源汽车等.它是未来汽车的发展方向.一个新能源汽车制造厂引进了一条新能源汽车整车装配流水线,这条流水线生产的新能源汽车数量![]() (辆)与创造的价值
(辆)与创造的价值![]() (万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到5625万元,则它可能生产的新能源汽车数量是___________辆.
(万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到5625万元,则它可能生产的新能源汽车数量是___________辆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B为椭圆![]() 上的两个动点,满足
上的两个动点,满足![]() .
.
(1)求证:原点O到直线AB的距离为定值;
(2)求![]() 的最大值;
的最大值;
(3)求过点O,且分别以OA,OB为直径的两圆的另一个交点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称函数
称函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在第(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象中心观察和预测:发生于甲地的沙尘暴一直向正南方向移动,其移动速度![]() 与时间
与时间![]() 的函数图象图所示,过线段
的函数图象图所示,过线段![]() 上一点
上一点![]() 作横轴的垂线
作横轴的垂线![]() ,梯形
,梯形![]() 在直线
在直线![]() 左侧部分的面积即为
左侧部分的面积即为![]() 内沙尘暴所经过的路程
内沙尘暴所经过的路程![]() .
.
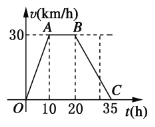
(1) 当![]() 时,求
时,求![]() 的值;
的值;
(2)将![]() 随
随![]() 变化的规律用数学关系式表示出来;
变化的规律用数学关系式表示出来;
(3)若乙城位于甲地正南方向,且距甲地![]() ,试判断这场沙尘暴是否会侵袭到乙城,如果会,在沙尘暴发生后多长时间它将侵袭到乙城?如果不会,请说明理由.
,试判断这场沙尘暴是否会侵袭到乙城,如果会,在沙尘暴发生后多长时间它将侵袭到乙城?如果不会,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com