
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若对于任意的![]() ,
,![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 有极小值
有极小值![]() ,没有极大值;(Ⅱ)
,没有极大值;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)将![]() 代入函数
代入函数![]() 的表达式,求出
的表达式,求出![]() 的导数,得到函数的单调区间,从而求出函数的极值即可;(Ⅱ)对于任意的
的导数,得到函数的单调区间,从而求出函数的极值即可;(Ⅱ)对于任意的![]() ,
,![]() 有
有![]() ,
,![]() .所以有
.所以有![]() 恒成立,即
恒成立,即![]() ,构造函数
,构造函数![]() ,利用导数求
,利用导数求![]() 最大值
最大值![]() ,只需
,只需![]() 即可.
即可.
试题解析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() 时,
时,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 是增函数,
是增函数,![]() ,
,![]() ,
,![]() 是减函数.
是减函数.
∴![]() 有极小值
有极小值![]() ,没有极大值.………………………5分
,没有极大值.………………………5分
(Ⅱ)![]() ,
,![]()
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,![]() 最大,………………7分
最大,………………7分
对于任意的![]() ,
,![]() .
.
![]() 恒成立,即对任意
恒成立,即对任意![]() ,
,![]() 恒成立,∴
恒成立,∴![]() ,…………9分
,…………9分
令![]() ,则
,则![]() .
.
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
当![]() 时,
时,![]() 最大值为
最大值为![]() ,…………………………11分
,…………………………11分
∴![]() 即
即![]() .……………………12分
.……………………12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2014年5月,我省南昌市遭受连日大暴雨天气,某网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票,按照南昌暴雨前后两个时间收集有效投票,暴雨后的投票收集了![]() 份,暴雨前的投票也收集了
份,暴雨前的投票也收集了![]() 份,所得统计结果如下表:
份,所得统计结果如下表:

已知工作人与从所有投票中任取一个,取到“不支持投入”的投票的概率为![]() .
.
(1)求列表中数据的值;
(2)能够有多大的把握认为南昌暴雨对民众是否赞成加大对修建城市地下排水设施的投入有关系?
附: 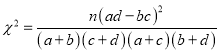
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F,右顶点为A,设离心率为e,且满足
的右焦点为F,右顶点为A,设离心率为e,且满足![]() ,其中O为坐标原点.
,其中O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点![]() 的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于命题![]() :存在一个常数
:存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() 恒成立.
恒成立.
(1)试给出这个常数![]() 的值;
的值;
(2)在(1)所得结论的条件下证明命题![]() ;
;
(3)对于上述命题,某同学正确地猜想了命题![]() :“存在一个常数
:“存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() ,
,![]() 恒成立.”观察命题
恒成立.”观察命题![]() 与命题
与命题![]() 的规律,请猜想与正数
的规律,请猜想与正数![]() ,
,![]() ,
,![]() ,
,![]() 相关的命题.
相关的命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据悉遵义市红花岗区、汇川区2017年现有人口总数为110万人,如果年自然增长率为![]() %,试解答以下问题:
%,试解答以下问题:
(1)写出经过![]() 年后,遵义市人口总数
年后,遵义市人口总数![]() (单位:万人)关于
(单位:万人)关于![]() 的函数关系式;
的函数关系式;
(2)计算10年以后遵义市人口总数(精确到0.1万人);
(3)计算经过多少年后遵义市人口将达到150万人(精确到1年)
(参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=x3+ax2-x+2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)对任意x∈(0,+∞),![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,其左、右顶点为
,其左、右顶点为![]() 、
、![]() ,椭圆与
,椭圆与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,
,![]() 的外接圆的圆心
的外接圆的圆心![]() 在直线
在直线![]() 上.
上.
(I)求椭圆![]() 的方程;
的方程;
(II)已知直线![]() :
:![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() ,垂足为
,垂足为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com