
����Ŀ�����г�����,�����س��м���ij�߲˼ӹ���,���²�����10����25��ʱ,�������ܳɱ�![]() ����Ԫ�����Կ����²���
����Ԫ�����Կ����²���![]() ���֣��Ķ��κ���.���²���Ϊ10��ʱ,���ܳɱ�Ϊ20��Ԫ�����²���Ϊ15��ʱ,���ܳɱ����Ϊ17.5��Ԫ.
���֣��Ķ��κ���.���²���Ϊ10��ʱ,���ܳɱ�Ϊ20��Ԫ�����²���Ϊ15��ʱ,���ܳɱ����Ϊ17.5��Ԫ.
��1��д�����ܳɱ�![]() ����Ԫ�������²���
����Ԫ�������²���![]() ���֣��ĺ�����ϵ��
���֣��ĺ�����ϵ��
��2����֪�ò�Ʒ���ۼ�Ϊÿ��1.6��Ԫ,��ô�²���Ϊ����ʱ,�ɻ��������
��3�����²���Ϊ���ٶ�ʱ, ÿ��ƽ���ɱ����,��ͳɱ��Ƕ�����Ԫ��
���𰸡���1��![]() ��
��![]() ������2���²���Ϊ23��ʱ���ɻ��������12.9��Ԫ����3���²���Ϊ20��ʱ��ÿ��ƽ���ɱ���ͣ���ͳɱ�Ϊ1��Ԫ.
������2���²���Ϊ23��ʱ���ɻ��������12.9��Ԫ����3���²���Ϊ20��ʱ��ÿ��ƽ���ɱ���ͣ���ͳɱ�Ϊ1��Ԫ.
��������
���⣨1���ɴ���ϵ�������![]() ��x=10��y=20����ɵ�
��x=10��y=20����ɵ�![]() ����2���������룭�ɱ���������Ϊ
����2���������룭�ɱ���������Ϊ![]() �ɵ�
�ɵ�![]() ��Ϊ���κ�������ֵ���ɣ���3��ƽ���ɱ���
��Ϊ���κ�������ֵ���ɣ���3��ƽ���ɱ���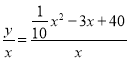 �ɻ�Ϊ
�ɻ�Ϊ![]() ���û�������ʽ����Сֵ��
���û�������ʽ����Сֵ��
����������⣺��1��![]() ��
��![]() �� 2��
�� 2��
��x=10��y=20������ʽ�ã�20=25a+17.5�����![]() 3��
3��
![]() ��
��![]() �� 4��
�� 4��
��2��������Ϊ![]() ��
��![]() 6��
6��
![]()
![]()
��Ϊ![]() �������²���Ϊ23��ʱ���ɻ��������12.9��Ԫ8��
�������²���Ϊ23��ʱ���ɻ��������12.9��Ԫ8��
��3��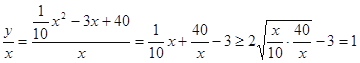 10��
10��
���ҽ���![]() ����
����![]() ʱ��ʽ��=������. 11��
ʱ��ʽ��=������. 11��
�ʵ��²���Ϊ20��ʱ��ÿ��ƽ���ɱ���ͣ���ͳɱ�Ϊ1��Ԫ. 12��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,��A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)��6���������ѡȡ3����,����3���㼰ԭ��O������������һ�������塱,�Ǹá����塱�����Ϊ�������V(���ѡȡ��3������ԭ����ͬһ��ƽ����,��ʱ�����塱�����V=0).
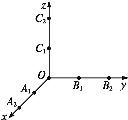
(1)��V=0�ĸ���;
(2)��V�ķֲ��м���ѧ����E(V).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��4������ϵ���������
��ֱ������xOy�У�ԲC1��x2+y2=4��ԲC2����x��2��2+y2=4��
��1������OΪ���㣬x��������Ϊ����ļ�����ϵ�У��ֱ�д��ԲC1 �� C2�ļ����귽�̣������ԲC1 �� C2�Ľ������꣨�ü������ʾ����
��2����ԲC1��C2�Ĺ����ҵIJ������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������������߷���:
(1)����(-2,3);
(2)������x����,���������ϵĵ�A(4,m)���ߵľ���Ϊ6.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У���������洹ֱ��
�У���������洹ֱ�� ![]() ����
����![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е�.
���е�.
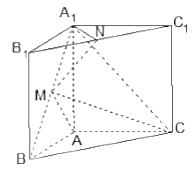
��1��֤���� ![]() ƽ��
ƽ��![]() ��
��
֤���� ![]() ƽ��
ƽ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A��{x|1<x<3}������B��{x|2m<x<1��m}��
(1)��m����1ʱ����A��B��
(2)��AB����ʵ��m��ȡֵ��Χ��
(3)��A��B������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʊ��30����ÿ�ɵĽ��۸�![]() ��Ԫ����ʱ��
��Ԫ����ʱ��![]() ���죩�����������
���죩�����������![]() ����
����![]() ������ͼ��ʾ�������߶��ϣ��ù�Ʊ��30���ڵ��ս�����
������ͼ��ʾ�������߶��ϣ��ù�Ʊ��30���ڵ��ս�����![]() ����ɣ���ʱ��
����ɣ���ʱ��![]() ���죩�IJ������������ʾ��
���죩�IJ������������ʾ��
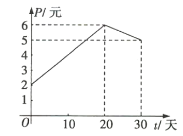
![]()
��1�������ṩ��ͼ��д���ù�Ʊÿ�ɵĽ��۸�![]() ��ʱ��
��ʱ��![]() ������ĺ�����ϵʽ��
������ĺ�����ϵʽ��
��2�����ݱ�������ȷ���ս�����![]() ��ʱ��
��ʱ��![]() ��һ�κ�����ϵʽ��
��һ�κ�����ϵʽ��
��3���ڣ�1����2���Ľ����£����ù�Ʊ���ս���Ϊ![]() ����Ԫ����д��
����Ԫ����д��![]() ����
����![]() �ĺ�����ϵʽ����������30���еڼ���Ľ����������Ƕ��٣�
�ĺ�����ϵʽ����������30���еڼ���Ľ����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ����g��x������2����㣬��a��ȡֵ��Χ��
����g��x������2����㣬��a��ȡֵ��Χ��
A. [�C1��0�� B. [0��+�ޣ� C. [�C1��+�ޣ� D. [1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ��4��4������ϵ��������̣���
��ֱ������ϵxOy�У���ԭ��OΪ���㣬x���������Ϊ���Ὠ��������ϵ����֪���ߦ�= ![]() ������
������ ![]() ��tΪ�������ཻ��A��B�����㣬���߶�AB���е��ֱ������Ϊ ��
��tΪ�������ཻ��A��B�����㣬���߶�AB���е��ֱ������Ϊ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com