

 的图形向右平移
的图形向右平移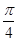 个单位后得到
个单位后得到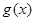 的图像,已知
的图像,已知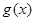 的部分图像如图所示,该图像与y轴相交于点
的部分图像如图所示,该图像与y轴相交于点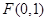 ,与x轴相交于点P、Q,点M为最高点,且
,与x轴相交于点P、Q,点M为最高点,且 的面积为
的面积为 .
.
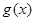 的解析式;
的解析式; 中,
中, 分别是角A,B,C的对边,
分别是角A,B,C的对边,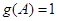 ,且
,且 ,求
,求 面积的最大值.
面积的最大值.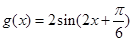 ;(2)
;(2)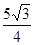 .
.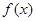 的图象向右平移
的图象向右平移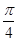 个单位得到
个单位得到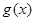 的解析式,由解析式得最大值M=2,利用三角形面积公式可得到
的解析式,由解析式得最大值M=2,利用三角形面积公式可得到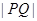 ,而周期
,而周期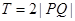 ,利用周期的计算公式得到
,利用周期的计算公式得到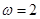 ,又因为
,又因为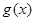 过
过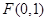 ,代入解析式得到
,代入解析式得到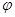 的值,从而得到
的值,从而得到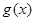 的解析式;第二问,先利用
的解析式;第二问,先利用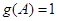 ,利用特殊角的三角函数值得到角A的大小,再利用余弦定理得到b和c的一个关系式,利用基本不等式得到
,利用特殊角的三角函数值得到角A的大小,再利用余弦定理得到b和c的一个关系式,利用基本不等式得到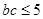 ,代入到三角形面积公式中,得到面积的最大值.
,代入到三角形面积公式中,得到面积的最大值.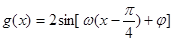
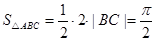 ,则
,则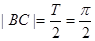 ,∴
,∴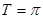 ,即
,即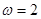 2分
2分 ,且
,且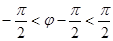 ,则
,则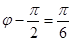 ,∴
,∴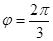 5分
5分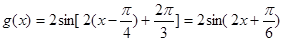 . 6分
. 6分 ,
,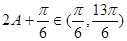 则
则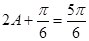 ,∴
,∴ 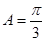 8分
8分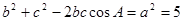 ,∴
,∴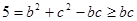 10分
10分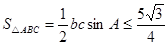 ,当且仅当
,当且仅当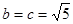 时,等号成立,故
时,等号成立,故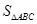 的最大值为
的最大值为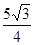 . 12分
. 12分

 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:不详 题型:解答题
 ,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.
,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π. ,f
,f =
= ,f
,f =-
=- ,求sin(α+β)的值.
,求sin(α+β)的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com