
【题目】(1)求![]() 的展开式中
的展开式中![]() 的系数及展开式中各项系数之和;
的系数及展开式中各项系数之和;
(2)从0,2,3,4,5,6这6个数字中任取4个组成一个无重复数字的四位数,求满足条件的四位数的个数.
【答案】(1)![]() (2)300
(2)300
【解析】试题分析:(1)直接利用二项展开式定理求解即可展开式中![]() 的系数,令
的系数,令![]() 即可得结果;(2)分选
即可得结果;(2)分选![]() ,不选
,不选![]() 两种情况讨论,再利用分类计数加法原理可得结果.
两种情况讨论,再利用分类计数加法原理可得结果.
试题解析:(1)∵![]() ,∴展开式中
,∴展开式中![]() 的系数为
的系数为![]() .
.
令![]() ,得各项系数之和为
,得各项系数之和为![]() .
.
(2)若不选0,则有![]() 个;
个;
若选0,则有![]() 个.
个.
故能组成![]() 个不同的四位数.
个不同的四位数.
【方法点晴】本题主要考查二项展开式定理的通项与系数及排列组合综合问题,属于中档题题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要从以下几个方面命题:(1)考查二项展开式的通项公式![]() ;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.
;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,当
,当![]()
![]() ,
,![]() 时,有
时,有![]() 成立.
成立.
(Ⅰ)判断![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅱ)若![]() 对所有的
对所有的![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列正确命题有__________.
①“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
②如果命题“![]() ”为假命题,则
”为假命题,则![]() 中至多有一个为真命题
中至多有一个为真命题
③设![]() ,若
,若![]() ,则
,则![]() 的最小值为
的最小值为![]()
④函数![]() 在
在![]() 上存在
上存在![]() ,使
,使![]() ,则a的取值范围
,则a的取值范围![]() 或
或![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
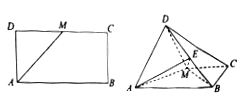
【题目】如图,已知长方形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)求证: ![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在何位置时,二面角
在何位置时,二面角![]() 的余弦值为
的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() .
.
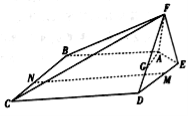
(1)已知点![]() 在线段
在线段![]() 上,确定
上,确定![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,
向上翻折,![]() 与
与![]() 恰好重合,求直线
恰好重合,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() .
.
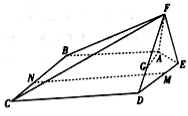
(1)已知点![]() 在线段
在线段![]() 上,确定
上,确定![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,
向上翻折,![]() 与
与![]() 恰好重合,求三棱锥
恰好重合,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 与
与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的圆的切线为
的圆的切线为![]() 是圆上异于
是圆上异于![]() 的一点,
的一点,![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 是
是![]() 的中点,延长
的中点,延长![]() 分别交
分别交![]() 于
于![]() .
.

(1)若点![]() ,求以
,求以![]() 为直径的圆的方程,并判断
为直径的圆的方程,并判断![]() 是否在圆上;
是否在圆上;
(2)当![]() 在圆上运动时,证明:直线
在圆上运动时,证明:直线![]() 恒与圆
恒与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在透明塑料制成的长方体![]() 容器内灌进一些水(未满),现将容器底面一边
容器内灌进一些水(未满),现将容器底面一边![]() 固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
①水的部分始终呈棱柱状;
②水面四边形![]() 的面积为定值;
的面积为定值;
③棱![]() 始终与水面
始终与水面![]() 平行;
平行;
④若![]() ,
, ![]() ,则
,则![]() 是定值.
是定值.
则其中正确命题的个数的是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com