
【题目】已知函数f(x)=Asin(ωx+φ)(A,ω>0,﹣π<φ<π)在一个周期内的图象如图所示. 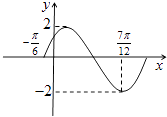
(1)求f(x)的表达式;
(2)在△ABC中,f(C+ ![]() )=﹣1且
)=﹣1且 ![]() <0,求角C.
<0,求角C.
【答案】
(1)解:由图可知函数的最大值是2,最小值是﹣2,
∴A=2,
∵ ![]() T=
T= ![]() +
+ ![]() =
= ![]() ,
,
∴T=π= ![]() ,可得:ω=2,
,可得:ω=2,
又∵f(x)过点(﹣ ![]() ,0),且根据图象特征得:﹣2×
,0),且根据图象特征得:﹣2× ![]() +φ=0+2kπ,k∈Z,
+φ=0+2kπ,k∈Z,
∴φ= ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
而﹣π<φ<π,
∴φ= ![]() .
.
∴f(x)=2sin(2x+ ![]() )
)
(2)解:∵f(x)=2sin(2x+ ![]() ),
),
∴f(C+ ![]() )=2sin(2C
)=2sin(2C ![]() )=﹣1,
)=﹣1,
∴sin(2C ![]() )=﹣
)=﹣ ![]() ,
,
因为C为三角形内角,
∴C= ![]() 或
或 ![]() ,
,
又∵ ![]() =abcosC<0,0<C<π,
=abcosC<0,0<C<π,
∴cosC<0, ![]() <C<π,
<C<π,
∴C= ![]()
【解析】(1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,从而求得函数f(x)的表达式.(2)利用(1)及f(C+ ![]() )=﹣1可得sin(2C
)=﹣1可得sin(2C ![]() )=﹣
)=﹣ ![]() ,结合角的范围可求C=
,结合角的范围可求C= ![]() 或
或 ![]() ,利用平面向量数量积的运算可求cosC<0,从而可求C的值.
,利用平面向量数量积的运算可求cosC<0,从而可求C的值.


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
【题目】动点![]() 分别到两定点
分别到两定点![]()
![]() 连线的斜率之乘积为
连线的斜率之乘积为![]() ,设
,设![]() 的轨迹为曲线
的轨迹为曲线![]() ,
, ![]() ,
, ![]() 分别为曲线
分别为曲线![]() 的左右焦点,则下列命题中:
的左右焦点,则下列命题中:
(1)曲线![]() 的焦点坐标为
的焦点坐标为![]() ,
, ![]() ;
;
(2)若![]() ,则
,则![]()
![]() ;
;
(3)当![]() 时,
时, ![]() 的内切圆圆心在直线
的内切圆圆心在直线![]() 上;
上;
(4)设![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中, ![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,
, ![]() 分别为
分别为![]() 与
与![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 上的射影是
上的射影是![]() 的重心.
的重心.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d>0.设{an}的前n项和为Sn,a1=1,S2·S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
查看答案和解析>>
科目:高中数学 来源: 题型:
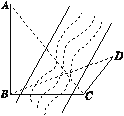
【题目】如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高是( )
A. 10m B. 10![]() m C. 10
m C. 10![]() m D. 10
m D. 10![]() m
m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图:
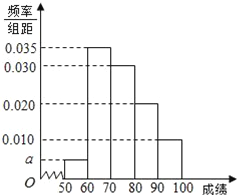
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高产品的年产量,某企业拟在2013年进行技术改革,经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3﹣ ![]() (k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)
(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)
(1)试确定k的值,并将2013年该产品的利润y万元表示为技术改革费用m万元的函数(利润=销售金额﹣生产成本﹣技术改革费用);
(2)该企业2013年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com