
【题目】如图,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ;
;
③![]() 是
是![]() ;
;
④平面![]() 平面
平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为30°.
所成角为30°.
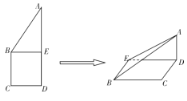
其中正确的有________.(填写你认为正确的序号)
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于甲、乙两个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,现该市有3位申请人在申请公租房:
(1)用合适的符号写出样本空间;
(2)求没有人申请甲片区房源的概率;
(3)求每个片区的房源都有人申请的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市预测2000年到2004年人口总数与年份的关系如下表所示
年份200x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十)万 | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,计算![]() ,用最小二乘法求出
,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
(2) 据此估计2005年该城市人口总数。
(参考数值:0×5+1×7+2×8+3×11+4×19=132,![]()
参考公式:用最小二乘法求线性回归方程系数公式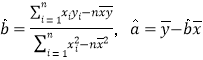 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知数列![]() 中,
中,![]() ,前项和
,前项和![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列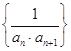 的前项和为
的前项和为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对一切正整数都成立?若存在,求出
对一切正整数都成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com