
如图,在三棱柱ABCA1B1C1中,A1B⊥平面ABC,AB⊥AC,且AB=AC=A1B=2.
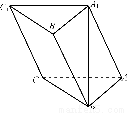
(1)求棱AA1与BC所成的角的大小;
(2)在棱B1C1上确定一点P,使二面角P-AB-A1的平面角的余弦值为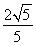 .
.
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第4课时练习卷(解析版) 题型:填空题
设a+b=2,b>0,则当a=________时,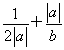 取得最小值.
取得最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:解答题
设z=2x+y,式中变量满足下列条件: 求z的最大值和最小值.
求z的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷(解析版) 题型:解答题
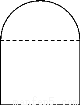
要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷(解析版) 题型:填空题
不等式ax2+bx+2>0的解集是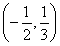 ,则a-b=________.
,则a-b=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
如图所示,直三棱柱ABCA1B1C1中,D、E分别是AB、BB1的中点,AA1=AC=CB=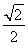 AB.
AB.
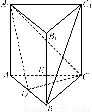
(1)证明:BC1∥平面A1CD;
(2)求二面角DA1CE的正弦值..
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4).设a= ,b=
,b= .
.
(1)求a和b的夹角θ;
(2)若向量ka+b与ka-2b互相垂直,求k的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:解答题
四面体的六条棱中,有五条棱长都等于a.
(1)求该四面体的体积的最大值;
(2)当四面体的体积最大时,求其表面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:解答题
在正三棱柱ABCA1B1C1中,点D是BC的中点,BC=BB1.
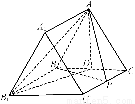
(1)若P是CC1上任一点,求证:AP不可能与平面BCC1B1垂直;
(2)试在棱CC1上找一点M,使MB⊥AB1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com