
【题目】如图,四棱锥![]() 中,
中,![]() 为等边三角形,
为等边三角形,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
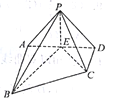
(1)求证:平面PEC![]() 平面EBC;
平面EBC;
(2)若![]() ,且二面角
,且二面角![]() 的平面角为
的平面角为![]() ,求实数
,求实数![]() 的值.
的值.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】有一种鱼的身体吸收汞,一定量身体中汞的含量超过其体重的1.00ppm(即百万分之一)的鱼被人食用后,就会对人体产生危害.在30条鱼的样本中发现的汞含量(单位:ppm)如下:
0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39 1.02
1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62 1.68
1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91 1.31
(1)请用合适的统计图描述上述数据,并分析这30条鱼的汞含量的分布特点;
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过你认为每批这种鱼的平均承含量都比1.00ppm大吗?
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是
是![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划投资A、B两种金融产品,根据市场调查与预测,A产品的利润与投资量成正比例,其关系如图1,B产品的利润与投资量的算术平方根成正比例,其关系如图2(注:利润与投资量的单位:万元).
(1)分别将A、B两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入A、B两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组数据:
125 121 123 125 127 129 125 128 130
129 126 124 125 127 126 122 124 125
126 128
(1)填写下面的频率分布表:
分组 | 频数累计 | 频数 | 频率 |
| |||
| |||
| |||
| |||
| |||
合计 |
(2)作出频率分布直方图.
(3)根据频率分布直方图或频率分布表求这组数据的众数、中位数和平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点.
上的两个不同点.
(1)若![]() ,且点
,且点![]() 所在直线方程为
所在直线方程为![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 的斜率之积为
的斜率之积为![]() ,线段
,线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接
,连接![]() 并廷长交椭圆
并廷长交椭圆![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选择合适的抽样方法抽样,写出抽样过程.
(1)有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取3个;
(2)有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的离心率为
(a>0,b>0)的离心率为![]() ,且
,且![]()
(1)求双曲线C的方程;
(2)已知直线![]() 与双曲线C交于不同的两点A,B且线段AB的中点在圆
与双曲线C交于不同的两点A,B且线段AB的中点在圆![]() 上,求m的值
上,求m的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合P={x|x(x-2)≥0},M={x|a<x<a+3}.
(1)求集合UP;
(2)若a=1,求集合P∩M;
(3)若UPM,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com