
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 由题意可判断a2>1,0<a2009<1,0<a2009<1<a2,从而公差d<0可判断③,两式相加整理可得a2+a2009=2,利用等差数列的性质可知a1+a2010=a2+a2009=2可判断①②,由公差d<0 可得a2+a2008>a2+a2009>a2+a2010,结合等差数列的性质,可得2a1005>2>2a1006,从而可得0<a1006<1<a1005,可判断④的正误.
解答 解:由(a2-1)3+2010(a2-1)=1,(a2009-1)3+2010(a2009-1)=-1
可得a2-1>0,-1<a2009-1<0即a2>1,0<a2009<1,
故可得等差数列的公差d<0,选项③a2009<a2正确;
把已知的两式相加可得(a2-1)3+2010(a2-1)+(a2009-1)3+2010(a2009-1)=0
整理可得(a2+a2009-2)•[(a2-1)2+(a2009-1)2-(a2-1)(a2009-1)+2010]=0
结合上面的判断可知(a2-1)2+(a2009-1)2-(a2-1)(a2009-1)+2010>0
故有a2+a2009=2,S2010=$\frac{2010({a}_{1}+{a}_{2010})}{2}$=2010•$\frac{{a}_{2}+{a}_{2009}}{2}$=2010,故选项②正确;
由于d<0,a2010<a2009<1,则S2009=S2010-a2010=2010-a2010>2009,故选项①错误;
由公差d<0 可得a2+a2008>a2+a2009>a2+a2010,结合等差数列的列的性质,
可得2a1005>2>2a1006,从而可得0<a1006<1<a1005,故s2009-s2=a3+a4+…+a2009=2007a1006>0,即选项④错误.
故选:B
点评 本题考查了等差数列的性质和求和公式,灵活利用结论是解决问题的关键,属中档题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
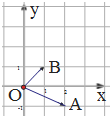 如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,设复数$z=\frac{z_1}{z_2}$,则z的共轭复数为( )
如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,设复数$z=\frac{z_1}{z_2}$,则z的共轭复数为( )| A. | $\frac{1}{2}-\frac{3}{2}i$ | B. | $\frac{1}{2}+\frac{3}{2}i$ | C. | 1-3i | D. | 1+3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|a≥2} | B. | {a|a≤2} | C. | {a|-1≤a≤2} | D. | {a|-1≤a<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com