分析:法一:(I)要证BC⊥面D
1DB,只需证明直线BC垂直面D
1DB内的两条相交直线D
1D、DB即可;
(II)取DC中点E,连接BE,D
1E.说明∠BD
1E为所求角,解三角形D
1BE,求D
1B与平面D
1DCC
1所成角的大小.
法二:建立空间直角坐标系,求出相关点的坐标,
(I)计算
•=0 , •=0就证明了直线BC垂直面D
1DB内的两条相交直线D
1D、DB,从而证明BC⊥面D
1DB.
(II)求出
和平面D
1DCC
1的法向量,计算
|cos<,>|=||,即可求D
1B与平面D
1DCC
1所成角的大小.
解答: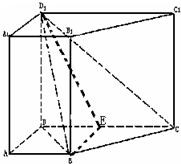
解:解法一:
(I)证明:∵ABCD-A
1B
1C
1D
1为直四棱柱,
∴D
1D⊥平面ABCD,
∴BC⊥D
1D.
∵AB∥CD,AB⊥AD.
∴四边形ABCD为直角梯形,
又∵AB=AD=1,CD=2,
可知BC⊥DB.
∵D
1D∩DB=D,
∴BC⊥平面D
1DB.(6分)
(II)取DC中点E,连接BE,D
1E.
∵DB=BC,
∴BE⊥CD.
∵ABCD-A
1B
1C
1D
1为直四棱柱,
∴ABCD⊥D
1DCC
1.
∴BE⊥D
1DCC
1.
∴D
1E为D
1B在平面D
1DCC
1上的射影,
∴∠BD
1E为所求角.
在Rt△D
1BE中,
BE=1,D1E=.
tan∠BD1E==.
∴所求角为
arctan.(14分)
解法二:
(I)证明:如图建立坐标系D-xyz,D(0,0,0),B(1,1,0),C(0,2,0),D
1(0,0,2).
∴
=(-1,1,0),=(0,0,2),=(1,1,0).
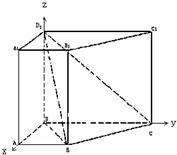
∵
•=0 , •=0,
∴BC⊥DD
1,BC⊥DB.
∵D
1D∩DB=D,
∴BC⊥平面D
1DB.(6分)
(II)
=(1,1,-2),A(1,0,0),=(1,0,0).
∵AD⊥平面D
1DCC
1,
∴平面D
1DCC
1的法向量
=(1,0,0),
∵
|cos<,>|=||==.
∴D
1B与平面D
1DCC
1所成角的大小为
arcsin.(14分)
点评:本题考查直线与平面垂直的判定,直线与平面所成的角,考查学生空间想象能力,逻辑思维能力,计算能力,是中档题.

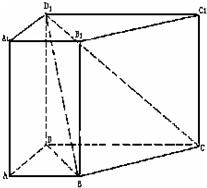 已知直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=AD=1,DD1=CD=2,AB⊥AD.
已知直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=AD=1,DD1=CD=2,AB⊥AD. 解:解法一:
解:解法一: ∵
∵

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案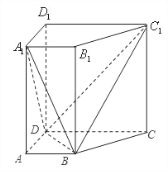 如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足
如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: 已知直四棱柱ABCD-A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点. (2010•宝山区模拟)已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.
(2010•宝山区模拟)已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.