
分析 (1)利用正弦定理化简后,根据和与差的公式可得B的大小.
(2)根据余弦定理建立关系,求出ac的值,即可得S△ABC的值.
解答 解:(1)由$\frac{cosB}{cosC}=-\frac{b}{2a+c}$,
根据正弦定理,可得:$\frac{cosB}{cosC}=-\frac{sinB}{2sinA+sinC}$,
2cosBsinA+cosBsinC=-sinBcosC,
即2cosBsinA=-sinA
∵0<A<π,sinA≠0.
∴cosB=$-\frac{1}{2}$
∵0<B<π,
∴$B=\frac{2π}{3}$
(2)$b=\sqrt{13},a+c=4$,由余弦定理:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
可得:-ac=a2+c2-13,即(a+c)2-ac-13=0
得:ac=3
那么三角形的面积${S_{△ABC}}=\frac{1}{2}acsinB=\frac{{3\sqrt{3}}}{4}$.
点评 本题考查三角形的正余弦定理和和与差公式的运用,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:解答题
给定函数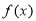 ,若对于定义域中的任意
,若对于定义域中的任意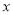 ,都有
,都有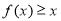 恒成立,则称函数
恒成立,则称函数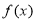 为“爬坡函数”.
为“爬坡函数”.
(1)证明:函数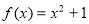 是爬坡函数;
是爬坡函数;
(2)若函数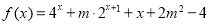 是爬坡函数,求实数m的取值范围;
是爬坡函数,求实数m的取值范围;
(3)若对任意的实数b,函数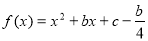 都不是爬坡函数,求实数c的取值范围.
都不是爬坡函数,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
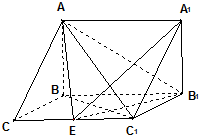 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=$\frac{π}{3}$
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=$\frac{π}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 200 | 400 | 200 | b | 100 | 1000 |
| 频率 | 0.2 | a | 0.2 | 0.1 | c | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com