
分析 由题意可得,x∈(0,$\frac{1}{4}$)时,函数y=4x的图象在函数y=logax的图象的下方,可得0<a<1.再根据它们的单调性可得4×($\frac{1}{4}$)≤loga$\frac{1}{4}$,解此对数不等式求得a的范围.
解答 解:∵不等式4x-logax<0对任意x∈(0,$\frac{1}{4}$)恒成立,
∴x∈(0,$\frac{1}{4}$)时,函数y=4x的图象在函数y=logax的图象的下方,
∴0<a<1.
再根据它们的单调性可得4×($\frac{1}{4}$)≤loga$\frac{1}{4}$,
即 logaa≤loga$\frac{1}{4}$,
∴a≥$\frac{1}{4}$
综上可得,$\frac{1}{4}$≤a<1,
故答案为:[$\frac{1}{4}$,1).
点评 本题主要考查对数不等式的解法,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
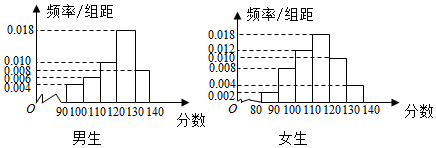 某中学一名数学老师对全班50名学生某次考试成绩分男女生进行统计(满分150分),其中120分(含120分)以上为优秀,绘制了如图所示的两个频率分布直方图:
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行统计(满分150分),其中120分(含120分)以上为优秀,绘制了如图所示的两个频率分布直方图:| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | 13 | 10 | 23 |
| 女生 | 7 | 20 | 27 |
| 总计 | 20 | 30 | 50 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
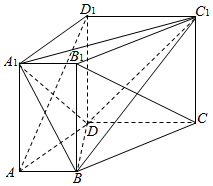 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,∠ADC=90°,AB∥CD,AD=CD=DD1=2AB=2.
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,∠ADC=90°,AB∥CD,AD=CD=DD1=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
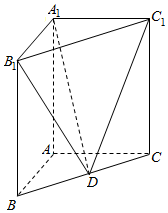 如图,在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点.
如图,在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com