练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，在中.，过作于延长到，使.沿将折起，将折到点的位置使平面平面.

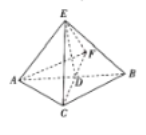
    （1）求证：平面平面；

    （2）求二面角的余弦值.

    【答案】（1）证明见解析；（2）

    【解析】

    根据题意,利用线面垂直的判定定理证明平面,再利用面面垂直的判定定理即可得证;

    由题意知,平面由线面垂直的性质知,两两垂直，以为原点，方向分别为轴，轴，轴正方向建立空间直角坐标系，分别求出平面和平面的法向量,则向量所成角的余弦值或其相反数即为所求.

    折到位置的过程中，.

    又,,

    所以平面而平面

    平面平面

    平面平面平面平面

    平面

    所以两两垂直，以为原点，

    方向分别为轴，轴，轴正方向建立空间直角坐标系，

    可得:，，

    设平面的一个法向量为，

    则

    令可得:，

    设平面的一个法向量为，

    则

    可得:，

    故，

    故二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某健身房为了解运动健身减肥的效果，调查了名肥胖者健身前（如直方图（1）所示）后（如直方图（2）所示）的体重（单位：）变化情况：

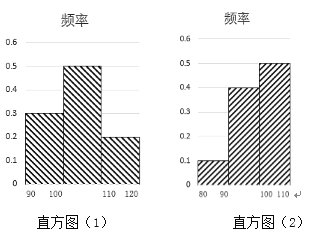
    对比数据，关于这名肥胖者，下面结论正确的是（ ）

    A.他们健身后，体重在区间内的人数较健身前增加了人

    B.他们健身后，体重原在区间内的人员一定无变化

    C.他们健身后，人的平均体重大约减少了

    D.他们健身后，原来体重在区间内的肥胖者体重都有减少

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，平面五边形是由边长为2的正方形与上底为1，高为直角梯形组合而成，将五边形沿着折叠，得到图2所示的空间几何体，其中.

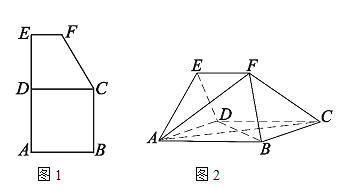
    （1）证明：平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】到2020年，我国将全面建立起新的高考制度，新高考采用模式，其中语文、数学、英语三科为必考科目，满分各150分，另外考生还要依据想考取的高校及专业的要求，结合自己的兴趣、爱好等因素，在思想政治、历史、地理、物理、化学、生物6门科目中自选3门（6选3）参加考试，满分各100分.为了顺利迎接新高考改革，某学校采用分层抽样的方法从高一年级1000名（其中男生550名，女生450名）学生中抽取了名学生进行调查.

    （1）已知抽取的名学生中有女生45名，求的值及抽取的男生的人数.

    （2）该校计划在高一上学期开设选修中的“物理”和“地理”两个科目，为了解学生对这两个科目的选课情况，对在（1）的条件下抽取到的名学生进行问卷调查（假定每名学生在这两个科目中必须选择一个科目，且只能选择一个科目），得到如下列联表.

    选择“物理”

    选择“地理”

    总计

    男生

    10

    女生

    25

    总计

    （i）请将列联表补充完整，并判断是否有以上的把握认为选择科目与性别有关系.

    （ii）在抽取的选择“地理”的学生中按性别分层抽样抽取6名，再从这6名学生中抽取2名，求这2名中至少有1名男生的概率.

    附：，其中.

    0.05

    0.01

    3.841

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某省确定从2021年开始，高考采用“”的模式，取消文理分科，即“3”包括语文、数学、外语，为必考科目；“1”表示从物理、历史中任选一门；“2”则是从生物、化学、地理、政治中选择两门，共计六门考试科目.某高中从高一年级2000名学生（其中女生900人）中，采用分层抽样的方法抽取名学生进行调查.

    （1）已知抽取的名学生中含男生110人，求的值及抽取到的女生人数；

    （2）学校计划在高二上学期开设选修中的“物理”和“历史”两个科目，为了了解学生对这两个科目的选课情况，对在（1）的条件下抽取到的名学生进行问卷调杳（假定每名学生在这两个科目中必须洗择一个科目且只能选择一个科目）.下表是根据调查结果得到的列联表，请将列联表补充完整，并判断是否有的把握认为选择科目与性别有关？说明你的理由；

    性别

    选择物理

    选择历史

    总计

    男生

    50

    女生

    30

    总计

    （3）在（2）的条件下，从抽取的选择“物理”的学生中按分层抽样抽取6人，再从这6名学生中抽取2人，对“物理”的选课意向作深入了解，求2人中至少有1名女生的概率.

    附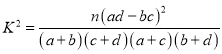：，其中.

    0.100

    0.050

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象在处的切线为.（为自然对数的底数）.

    （1）求，的值；

    （2）当时，求证：；

    （3）若对任意的恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《张丘建算经》是中国古代的著名数学著作，该书表明：至迟于公元5世纪，中国已经系统掌握等差数列的相关理论，该书上卷22题又“女工善织问题”：“今有女善织，日益功疾，初日织五尺，今一月曰织九匹三丈，问日益几何？”，大概意思是：有一个女工人善于织布，每天织布的尺数越来越多且成等差数列，第一天知5尺，30天共织九匹三丈，问每天增加的织布数目是多少寸？答案是__________寸．（注：当时一匹为四丈，一丈为十尺，一尺为十寸，结果四舍五入精确到寸）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中,曲线C的参数方程为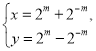(m为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθρsinθ2=0.

    (1)求C和l的直角坐标方程;

    (2)设直线l与曲线C的公共点为P,Q,求|PQ|.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正三棱柱的所有棱长都为，是的中点，在边上，.

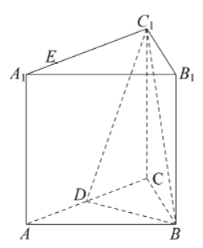
    （1）证明：平面平面；

    （2）若是侧面内的动点，且平面.

    ①在答题卡中作出点的轨迹，并说明轨迹的形状（不需要说明理由）；

    ②求三棱锥的体积.

    查看答案和解析>>

    同步练习册答案