
已知函数
(1)求函数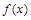 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(2)求函数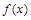 单调递增区间;
单调递增区间;
(3)若
 ∈[1,1],使得
∈[1,1],使得 (e是自然对数的底数),求实数
(e是自然对数的底数),求实数 的取值范围.
的取值范围.
(1)函数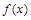 在点
在点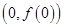 处的切线方程为
处的切线方程为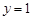 ;(2)函数
;(2)函数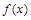 单调递增区间
单调递增区间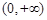 ;
;
(3)实数a的取值范围是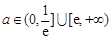 .
.
解析试题分析:⑴ 先根据函数解析式求出
科目:高中数学
来源:
题型:解答题
已知函数f(x)=
科目:高中数学
来源:
题型:解答题
某商场对A品牌的商品进行了市场调查,预计2012年从1月起前x个月顾客对A品牌的商品的需求总量P(x)件与月份x的近似关系是:
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
某家具厂生产一种儿童用组合床柜的固定成本为20000元,每生产一组该组合床柜需要增加投入100元,已知总收益满足函数:
科目:高中数学
来源:
题型:解答题
噪声污染已经成为影响人们身体健康和生活质量的严重问题.实践证明,声音强度
科目:高中数学
来源:
题型:解答题
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区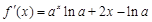 ,把
,把 代入求出斜率,进而求得切线方程;⑵ 因为当
代入求出斜率,进而求得切线方程;⑵ 因为当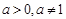 时,总有
时,总有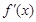 在
在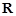 上是增函数, 又
上是增函数, 又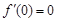 ,所以函数
,所以函数 的单调增区间为
的单调增区间为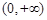 ;⑶ 要使
;⑶ 要使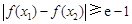 成立,只需
成立,只需 成立即可;再分
成立即可;再分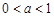 和
和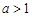 两种情况讨论即可.
两种情况讨论即可.
试题解析:⑴ 因为函数 ,
,
所以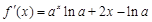 ,
,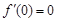 , 2分
, 2分
又因为 ,所以函数
,所以函数 在点
在点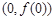 处的切线方程为
处的切线方程为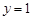 . 4分
. 4分
⑵ 由⑴,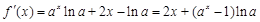 .
.
因为当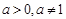 时,总有
时,总有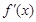 在
在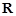 上是增函数,
上是增函数,
又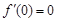 ,所以不等式
,所以不等式 的解集为
的解集为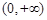 ,
,
故函数 的单调增区间为
的单调增区间为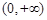 8分
8分
⑶ 因为存在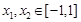 ,使得
,使得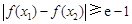 成立,
成立,
而当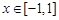 时,
时, ,
,
所以只要 即可 9分
即可 9分
又因为 ,
,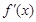 ,
, 的变化情况如下表所示:
的变化情况如下表所示:


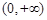
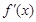


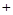

减函数 极小值 

给力闯关100分系列答案

精英教程全能卷系列答案
课程达标冲刺100分系列答案

百分金卷夺冠密题系列答案
微课堂百分大闯关系列答案
特级教师优化试卷系列答案

名师金考卷系列答案
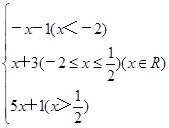 .
.
(1)求函数f(x)的最小值;
(2)已知m∈R,命题p:关于x的不等式f(x)≥m2+2m-2对任意m∈R恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
P(x)= x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
(1)写出第x月的需求量f(x)的表达式;
(2)若第x月的销售量g(x)=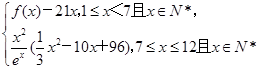
(单位:件),每件利润q(x)元与月份x的近似关系为:q(x)=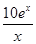 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数 ,
,
(1)求证:当 满足条件
满足条件 时,对于
时,对于 ,
,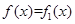 ;
;
(2)设 是两个实数,满足
是两个实数,满足 ,且
,且 ,若
,若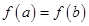 ,求函数
,求函数 在区间
在区间 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间 的长度定义为
的长度定义为 )
)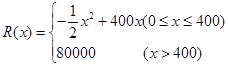 ,其中
,其中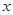 是组合床柜的月产量.
是组合床柜的月产量.
(1)将利润 元表示为月产量
元表示为月产量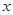 组的函数;
组的函数;
(2)当月产量为何值时,该厂所获得利润最大?最大利润是多少?(总收益=总成本+利润).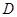 (分贝)由公式
(分贝)由公式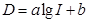 (
(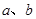 为非零常数)给出,其中
为非零常数)给出,其中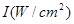 为声音能量.
为声音能量.
(1)当声音强度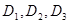 满足
满足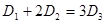 时,求对应的声音能量
时,求对应的声音能量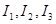 满足的等量关系式;
满足的等量关系式;
(2)当人们低声说话,声音能量为 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为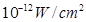 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.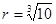 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.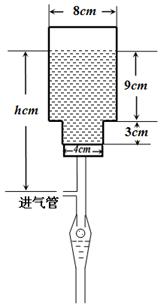
(1)如果瓶内的药液恰好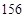 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后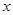 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为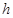 (单位:厘米),已知当
(单位:厘米),已知当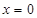 时,
时,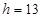 .试将
.试将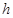 表示为
表示为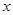 的函数.(注:
的函数.(注: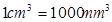 )
)
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号