练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．f（x）=x2-2ax，当a＜1时，对1＜x1＜x2，恒有|f（x1）-f（x2）|＞2|x1-x2|，则实数a的取值范围是a≤0．

    分析 求出：|f（x1）-f（x2）|=|x1-x2||x1+x2-2a|，对不等式整理得：|x1+x2-2a|＞2，解绝对值不等式即可．

    解答 解：|f（x1）-f（x2）|
    =|x1-x2||x1+x2-2a|，
    ∴|x1-x2||x1+x2-2a|＞2|x1-x2|，
    ∴|x1+x2-2a|＞2，
    ∴x1+x2-2a＞2或x1+x2-2a＜-2（不成立），
    ∴x1+x2＞2a+2，
    ∵x1+x2＞2，
    ∴2a+2≤2，
    ∴a≤0．
    故a的范围为a≤0．

    点评 考查了绝对值不等式的求解，属于基础题型，应熟练掌握．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

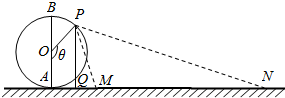    6．如图，摩天轮的半径OA为50m，它的最低点A距地面的高度忽略不计．地面上有一长度为240m的景观带MN，它与摩天轮在同一竖直平面内，且AM=60m．点P从最低点A处按逆时针方向转动到最高点B处，记∠AOP=θ，θ∈（0，π）．
    （Ⅰ）当θ=$\frac{2π}{3}$ 时，求点P距地面的高度PQ；
    （Ⅱ）设y=tan∠MPN，写出用θ表示y的函数关系式，并求y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}+\frac{3}{4}，}&{x≥2}\\{lo{g}_{2}x，}&{0＜x＜2}\end{array}\right.$，若关于x的方程f（x）-k=0有且只有1个根，则实数k的取值范围是k≤$\frac{3}{4}$或k=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．等比数列{an}中，a1，a5是关于x方程x2-bx+c=0的两个根，其中点（c，b）在直线y=x+1上，且c=$\int_0^3$t2dt，则a3的值是3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．设集合A={x|-3≤2x-1≤3}，集合B为函数y=lg（x-1）的定义域，则A∩B=（1，2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

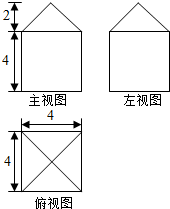
    1．一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是（　　）
    A．（80+16$\sqrt{2}$）cm2B．96cm2C．（96+16$\sqrt{2}$）cm2D．112cm2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．高为2的圆柱侧面积为4π，此圆柱的体积为2π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．函数y=$\sqrt{3}$sinx-cosx-2（x＞0）的值域是[-4，0]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=ln$\frac{1+x}{1-x}$．
    （1）求函数f（x）的定义域；
    （2）求使函数f（x）＞0的x的取值范围．

    查看答案和解析>>

    同步练习册答案