
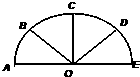
 如图,在以AE=2为直径的半圆周上,B,C,D分别为弧AE的四等分点.
如图,在以AE=2为直径的半圆周上,B,C,D分别为弧AE的四等分点.分析 (1)求出$\overrightarrow{a}$在$\overrightarrow{OA}$上的射影为正的事件个数,进而根据概率定义,计算即可;
(2)通过列举法,列出所有满足条件的向的基本事件数,然后观察符合条件的基本事件,计算即可.
解答 解:(1)以O点为起点,从A,B,C,D,E,这5个点中任取一点为终点得到一个向量$\overrightarrow{a}$,
所有的基本事件有:$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,$\overrightarrow{OD}$,$\overrightarrow{OE}$,共5个;
其中满足$\overrightarrow{a}$在$\overrightarrow{OA}$上的射影为正的有$\overrightarrow{OA}$,$\overrightarrow{OB}$,共2个;
∴满足$\overrightarrow{a}$在$\overrightarrow{OA}$上的射影为正的概率P=$\frac{2}{5}$;
(2)以O点为起点,从A,B,C,D,E,这5个点中任取两点分别为终点得到两个向量所有的基本事件有:
($\overrightarrow{OA}$,$\overrightarrow{OB}$),($\overrightarrow{OA}$,$\overrightarrow{OC}$),($\overrightarrow{OA}$,$\overrightarrow{OD}$),($\overrightarrow{OA}$,$\overrightarrow{OE}$),($\overrightarrow{OB}$,$\overrightarrow{OC}$),
($\overrightarrow{OB}$,$\overrightarrow{OD}$),($\overrightarrow{OB}$,$\overrightarrow{OE}$),($\overrightarrow{OC}$,$\overrightarrow{OD}$),($\overrightarrow{OC}$,$\overrightarrow{OE}$),($\overrightarrow{OD}$,$\overrightarrow{OE}$),共10个,
其中这两个向量垂直的有:($\overrightarrow{OA}$,$\overrightarrow{OC}$),($\overrightarrow{OB}$,$\overrightarrow{OD}$),($\overrightarrow{OC}$,$\overrightarrow{OE}$),共3个,
故这两个向量垂直的概率P=$\frac{3}{10}$.
点评 本题主要考查了概率的求法以及向量的有关知识,属于基础题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个红球与都是黑球 | B. | 至少有一个红球与恰有一个黑球 | ||
| C. | 至少有一个红球与至少有一个黑球 | D. | 恰有一个红球与恰有两个红球 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或x>1} | D. | {x|x<-1或0<x<1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com