
【题目】△ABC的内角A,B,C的对边分别为a,b,c,且cosAcosC﹣cos(A+C)=sin2B. (Ⅰ)证明:a,b,c成等比数列;
(Ⅱ)若角B的平分线BD交AC于点D,且b=6,S△BAD=2S△BCD , 求BD.
【答案】解:(Ⅰ)证明:∵cosAcosC﹣cos(A+C)=sin2B. ∴cosAcosC﹣(cosAcosC﹣sinAsinC)=sin2B,可得:sinAsinC=sin2B,
∴由正弦定理可得:b2=ac,
∴a,b,c成等比数列;
(Ⅱ)如图,∵角B的平分线BD交AC于点D,且b=6,可得:AD+CD=6,
∵S△BAD=2S△BCD , 可得:AD=2CD,
∴解得:AD=4,CD=2,
∵由(Ⅰ)可得:b2=ac=36,
∵ ![]() =
= ![]() ,可得:AB=2BC,即c=2a,
,可得:AB=2BC,即c=2a,
∴解得:a=3 ![]() ,c=6
,c=6 ![]() ,
,
∴cosA= ![]() =
= ![]() ,
,
∴BD= ![]() =2
=2 ![]() .
.
【解析】(Ⅰ)利用两角和的余弦函数公式化简已知等式可得sinAsinC=sin2B,由正弦定理可得:b2=ac,即可得证.(Ⅱ)由已知可得:AD+CD=6,由三角形面积公式可得AD=2CD,从而可求AD=4,CD=2,由(Ⅰ)可得:b2=36,利用角平分线的性质可得AB=2BC,即c=2a,从而可求a,c的值,进而利用余弦定理可求cosA,即可由余弦定理求得BD的值.
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列{an}中,a1=1,且a1 , a3 , a9成等比数列.
(1)求数列{an}的通项公式;
(2)设bn= ![]() +n,求数列Sn的前Sn项和Sn .
+n,求数列Sn的前Sn项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个问题:①x,输出它的绝对值.②求面积为6的正方形的周长.③求三个数a,b,c中最大数.④求函数![]() 的函数值.其中不需要用条件语句来描述其算法的有 个.
的函数值.其中不需要用条件语句来描述其算法的有 个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
[85,95) | ① | 0.025 |
[95,105) | 0.050 | |
[105,115) | 0.200 | |
[115,125) | 12 | 0.300 |
[125,135) | 0.275 | |
[135,145) | 4 | ② |
[145,155] | 0.050 | |
合计 | ③ |
(1)根据图表,①②③处的数值分别为、、;
(2)在所给的坐标系中画出[85,155]的频率分布直方图; 
(3)根据题中信息估计总体落在[125,155]中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率;
(2)检验结束后,甲、乙两名运动员的成绩如下:
甲:70,68,74,71,72
乙:70,69,70,74,72
根据两组数据完成图示的茎叶图,并通过计算说明哪位运动员的成绩更稳定.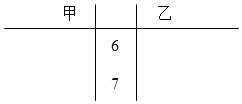
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com