
【题目】若![]() ,不等式
,不等式![]() 恒成立,则正实数
恒成立,则正实数![]() 的取值范围是_____.
的取值范围是_____.
【答案】![]()
【解析】
由题意可得(eλx![]() )min≥0,设f(x)=eλx
)min≥0,设f(x)=eλx![]() ,x>0,求出导数和单调区间、极小值点m和最小值点,可令最小值为0,解方程可得m,λ,进而得到所求最小值.
,x>0,求出导数和单调区间、极小值点m和最小值点,可令最小值为0,解方程可得m,λ,进而得到所求最小值.
实数λ>0,若对任意的x∈(0,+∞),不等式eλx![]() 0恒成立,
0恒成立,
即为(eλx![]() )min≥0,
)min≥0,
设f(x)=eλx![]() ,x>0,f′(x)=λeλx
,x>0,f′(x)=λeλx![]() ,
,
令f′(x)=0,可得eλx![]() ,
,
由指数函数和反比例函数在第一象限的图象,
可得y=eλx和y![]() 有且只有一个交点,
有且只有一个交点,
设为(m,n),当x>m时,f′(x)>0,f(x)递增;
当0<x<m时,f′(x)<0,f(x)递减.
即有f(x)在x=m处取得极小值,且为最小值.
即有eλm![]() ,令eλm
,令eλm![]() 0,
0,
可得m=e,λ![]() .
.
则当λ![]() 时,不等式eλx
时,不等式eλx![]() 0恒成立.
0恒成立.
故答案为![]() .
.


科目:高中数学 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]()
③由![]() ,满足
,满足![]() ,推出
,推出![]() 是奇函数;
是奇函数;
④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②④B. ①③④C. ②④D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教育部门为了了解某地区高中学生每周的课外羽毛球训练的情况,随机抽取了该地区50名学生进行调查,其中男生25人.将每周课外训练时间不低于8小时的学生称为“训练迷”,低于8小时的学生称为“非训练迷”.已知“训练迷”中有15名男生.根据调查结果绘制的学生每周课外训练时间的频率分布直方图(时间单位为小时)如图所示.
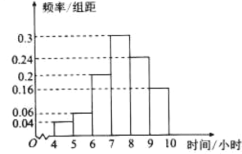
(1)根据图中数据估计该地区高中学生每周课外训练的平均时间(说明:同一组中的数据用该组区间的中间值作代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有99.5%的把握认为“训练迷”与性别有关?
列联表,并判断是否有99.5%的把握认为“训练迷”与性别有关?
非训练迷 | 训练迷 | 合计 | |
男 | |||
女 | |||
合计 |
(3)将每周课外训练时间为4-6小时的称为“业余球迷”,已知调查样本中,有3名“业余球迷”是男生,若从“业余球迷”中任意选取2人,求至少有1名男生的概率.
附: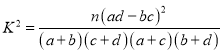 .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①相关指数![]() 越小,则残差平方和越小,模型的拟合效果越好.
越小,则残差平方和越小,模型的拟合效果越好.
②在![]() 的列联表中我们可以通过等高条形图直观判断两个变量是否有关.
的列联表中我们可以通过等高条形图直观判断两个变量是否有关.
③残差点比较均匀地落在水平带状区域内,带状区域越窄,说明模型拟合精度越高.
④两个随机变量相关性越强,则相关系数r越接近1.
其中正确命题的个数为( ).
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13s与19s之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13s且小于14s;第二组,成绩大于等于14s且小于15s;……;第六组,成绩大于等于18s且小于等于19s.如图是按上述分组方法得到的频率分布直方图.设成绩小于17s的学生人数占全班总人数的百分比为![]() ,成绩大于等于15s且小于17s的学生人数为
,成绩大于等于15s且小于17s的学生人数为![]() ,平均成绩为
,平均成绩为![]() ,则从频率分布直方图中可分析出
,则从频率分布直方图中可分析出![]() ,
,![]() ,
,![]() 的值分别为( )
的值分别为( )

A.90%,35,15.86B.90%,45,15.5
C.10%,35,16D.10%,45,16.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中,正确的是( )
A.命题“![]() ”的否定是“
”的否定是“![]() ”
”
B.若命题“![]() ”为真命题,则命题“
”为真命题,则命题“![]() ”为真命题
”为真命题
C.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D.“![]() ”是“命题‘
”是“命题‘![]() ’为真命题”的充分不必要条件
’为真命题”的充分不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com