【题目】（本小题满分14分）已知椭圆
的左焦点为
，右顶点为
，点
的坐标为
，
的面积为
.
（I）求椭圆的离心率；
（II）设点
在线段
上，
，延长线段
与椭圆交于点
，点
，
在
轴上，
，且直线
与直线
间的距离为
，四边形
的面积为
.
（i）求直线
的斜率；
（ii）求椭圆的方程.
【答案】（1）
（2）（ⅰ）
（ⅱ）
【解析】（Ⅰ）设椭圆的离心率为e.由已知，可得
.又由
，可得
，即
.又因为
，解得
.
所以，椭圆的离心率为
（Ⅱ）（ⅰ）依题意，设直线FP的方程为
，则直线FP的斜率为
.
由（Ⅰ）知
，可得直线AE的方程为
，即
，与直线FP的方程联立，可解得
，即点Q的坐标为
.
由已知|FQ|=
，有
，整理得
，所以
，即直线FP的斜率为
.
（ii）由
，可得
，故椭圆方程可以表示为
.
由（i）得直线FP的方程为
，与椭圆方程联立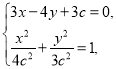
消去
，整理得
，解得
（舍去），或
.因此可得点
，进而可得
，所以
.由已知，线段
的长即为
与
这两条平行直线间的距离，故直线和都垂直于直线
.
因为
，所以
，所以
的面积为
，同理
的面积等于
，由四边形
的面积为
，得
，整理得
，又由
，得
.
所以，椭圆的方程为.
科目：高中数学 来源： 题型：
【题目】一个盒子装有六张卡片，上面分别写着如下六个函数:
.
（Ⅰ）从中任意拿取
张卡片,其中至少有一张卡片上写着的函数为奇函数,在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率；
（Ⅱ）现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数
的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校为缓解高三学生的高考压力，经常举行一些心理素质综合能力训练活动，经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试，并将其成绩分为
、
、
、
、
五个等级，统计数据如图所示（视频率为概率），根据以上抽样调查数据，回答下列问题：
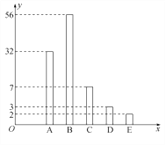
（1）试估算该校高三年级学生获得成绩为
的人数；
（2）若等级
、
、
、
、
分别对应100分、90分、80分、70分、60分，学校要求平均分达90分以上为“考前心理稳定整体过关”，请问该校高三年级目前学生的“考前心理稳定整体”是否过关？
（3）为了解心理健康状态稳定学生的特点，现从
、
两种级别中，用分层抽样的方法抽取11个学生样本，再从中任意选取3个学生样本分析，求这3个样本为
级的个数
的分布列与数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】△ABC中，a、b、c分别为∠A，∠B，∠C的对边，如果a、b、c成等差数列，∠B=30°，△ABC的面积为 
，那么b等于（ ）
A.
B.1+ 
C.
D.2+
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一盒中装有各色球12只，其中5个红球，4个黑球，2个白球，1个绿球；从中随机取出1球．求：
（1）取出的1球是红球或黑球的概率；
（2）取出的1球是红球或黑球或白球的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】四面体ABCD中，AB和CD为对棱．设AB=a，CD=b，且异面直线AB与CD间的距离为d，夹角为θ．
（Ⅰ）若θ= 
，且棱AB垂直于平面BCD，求四面体ABCD的体积；
（Ⅱ）当θ= 时，证明：四面体ABCD的体积为一定值；
（Ⅲ）求四面体ABCD的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
