分析:(1)由题意,可由AB⊥面BC1,证得AB⊥BE,再由题设条件用勾股定理证出∠BEB1=90°,得出BE⊥EB1,即可得出结论;
(2)求二面角A-EB1-A1的大小要先作出其平面角,由题设条件及图形知,可证得∠AEB1为二面角A-EB1-A1的平面角,再由条件求角;
(3)求点到面的距离问题一般可以用等体积法求解,由图形知VA1-AEB1=VE-A1B1A,求出相关的量,即可得出点到面的距离.
解答:解:(1)证明:∵AB⊥BC,AB⊥BB
1,∴AB⊥面BC
1,∴AB⊥BE
∵BE=B
1E=
,BB
1=2,∴∠BEB
1=90°,∴BE⊥EB
1BE是异面直线AB与EB
1的公垂
(2)∵AB⊥面BC
1,BE⊥EB
1,∴AE⊥EB
1∴∠AEB
1为二面角A-EB
1-A
1的平面角
∵AB=
,BE=
,∴∠AEB=45°
∵面A
1B
1E⊥面BCB
1C
1,∴二面角A-EB
1-A
1为45°
(3)设点A
1到面AEB
1的距离为h,
由上证及题设条件知
S△AEB1=•AE•EB1=,
又
S△A1B1A=•A1B1•AA1=,点E到面A
1B
1A的距离是1
∵
VA1-AEB1=VE-A1B1A,
∴
×
×h=
×
×1
∴h=1
即点A
1到面AEB
1的距离.
点评:本题考查二面角的求法,解答本题关键是掌握住二面角求法步骤,作角,证角,求角,其中第二步证明过程容易漏掉,解题时要谨记,本题考查到点到面距离的求法,注意总结此问题的解法规律及解法步骤,点到面距离的求解是立体几何中一类重要题型.这几年高考中也多有涉及,本题思维量与运算量不少,解题时要认真.

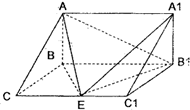 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,E为棱CC1的中点,已知AB=
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,E为棱CC1的中点,已知AB=

 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB= 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.