
【题目】如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E,F,G分别在棱SA,SB,SC上,且平面EFG∥平面ABC,点E为SA的中点.求证:
(Ⅰ)AF⊥平面SBC;
(Ⅱ)SA⊥BC.

【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】
(Ⅰ)由平面EFG∥平面ABC证得![]() ,即可说明点
,即可说明点![]() 是
是![]() 的中点,即可证得AF⊥SB,利用平面SAB⊥平面SBC即可证得AF⊥平面SBC,问题得证。
的中点,即可证得AF⊥SB,利用平面SAB⊥平面SBC即可证得AF⊥平面SBC,问题得证。
(Ⅱ)由(Ⅰ)中结论可证得BC⊥AF,结合BA⊥BC即可证得BC⊥平面SAB,问题得证。
证明:(Ⅰ)![]() 平面EFG∥平面ABC,
平面EFG∥平面ABC,
平面EFG![]() 平面
平面![]() =
=![]() ,平面ABC
,平面ABC![]() 平面
平面![]() =
=![]() ,
,
![]()
![]() ,又点
,又点![]() 是
是![]() 的中点
的中点
![]() 点
点![]() 是
是![]() 的中点,
的中点,

又AS=AB,
![]() AF⊥SB
AF⊥SB
∵在三棱锥S-ABC中,平面SAB⊥平面SBC,平面SAB∩平面SBC=SB,
∴AF⊥平面SBC.
(Ⅱ)∵AF⊥平面SBC,BC平面SBC,
∴BC⊥AF,
∵BA⊥BC.BA∩AF=A,
∴BC⊥平面SAB,
∵SA平面SAB,∴SA⊥BC.


科目:高中数学 来源: 题型:
【题目】设等比数列{an}的公比为q,其前n项之积为Tn,并且满足条件:a1>1,a2 016a2 017>1, ![]() .给出下列结论:(1)0<q<1;(2)a2 016a2 018-1>0;(3)T2 016是数列{Tn}中的最大项;(4)使Tn>1成立的最大正整数n为4 031.其中正确的结论为( )
.给出下列结论:(1)0<q<1;(2)a2 016a2 018-1>0;(3)T2 016是数列{Tn}中的最大项;(4)使Tn>1成立的最大正整数n为4 031.其中正确的结论为( )
A. (2)(3) B. (1)(3)
C. (1)(4) D. (2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
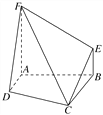
【题目】如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,二面角FABD是直二面角,BE∥AF,BC∥AD,AF=AB=BC=2,AD=1.
(1)证明:在平面BCE上,一定存在过点C的直线l与直线DF平行;
(2)求二面角FCDA的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人,斐波那契数列被誉为是最美的数列,斐波那契数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( )
A.已知直线![]() 和平面
和平面![]() ,若点
,若点![]() ,点
,点![]() 且
且![]() ,
,![]() ,则
,则![]()
B.若三条直线两两相交,则三条直线确定一个平面
C.若直线![]() 不平行于平面
不平行于平面![]() ,且
,且![]() ,则
,则![]() 内的所有直线与
内的所有直线与![]() 都不相交
都不相交
D.若直线![]() 和
和![]() 不平行,且
不平行,且![]() ,
,![]() ,
,![]() ,则l至少与
,则l至少与![]() ,
,![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,C是圆O上一点,AC=BC,且PA⊥平面ABC,E是AC的中点,F是PB的中点,PA=![]() ,AB=2.求:
,AB=2.求:
(Ⅰ)异面直线EF与BC所成的角;
(Ⅱ)点A到平面PBC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在一个实数![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的一个不动点,设函数
的一个不动点,设函数![]() (
(![]() ,
, ![]() 为自然对数的底数),定义在
为自然对数的底数),定义在![]() 上的连续函数
上的连续函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() .若存在
.若存在![]() ,且
,且![]() 为函数
为函数![]() 的一个不动点,则实数
的一个不动点,则实数![]() 的取值范围为( )
的取值范围为( )
A. 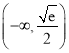 B.
B. 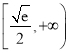 C.
C. 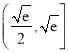 D.
D. 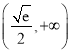
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市11月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月12日中的某一天到达该市,并停留3天.

(1)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气重度污染的天数,求X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com