
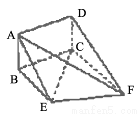
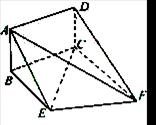
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,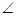 BCF=
BCF=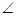 CEF=
CEF=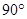 ,AD=
,AD=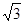 ,EF=2.
,EF=2.
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为 .
.
(1)见解析;(2)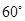 .
.
【解析】由于理科有空间向量的知识,在解决立体几何试题时就有两套根据可以使用,这为考生选择解题方案提供了方便,但使用空间向量的方法解决立体几何问题也有其相对的缺陷,那就是空间向量的运算问题,空间向量有三个分坐标,在进行运算时极易出现错误,而且空间向量方法证明平行和垂直问题的优势并不明显,所以在复习立体几何时,不要纯粹以空间向量为解题的工具,要注意综合几何法的应用。(1)只要过点 作
作 的平行线即可;(2)由于点
的平行线即可;(2)由于点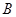 是点
是点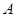 在平面
在平面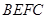 内的射影,只要过点
内的射影,只要过点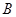 作
作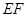 的垂线即可很容易地作出二面角
的垂线即可很容易地作出二面角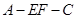 的平面角,剩下的就是具体的计算问题。或者建立空间直角坐标系,使用法向量的方法求解。
的平面角,剩下的就是具体的计算问题。或者建立空间直角坐标系,使用法向量的方法求解。
方法一:(Ⅰ)证明:过点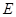 作
作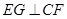 交
交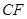 于
于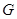 ,连结
,连结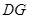 ,
,

可得四边形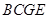 为矩形,又
为矩形,又 为矩形,所以
为矩形,所以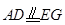 ,从而四边形
,从而四边形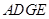 为平行四边形,故
为平行四边形,故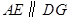 .因为
.因为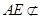 平面
平面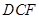 ,
,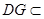 平面
平面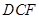 ,
,
所以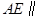 平面
平面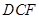 .………6分
.………6分
(Ⅱ)解:过点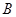 作
作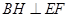 交
交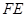 的延长线于
的延长线于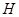 ,连结
,连结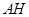 .
.
由平面 平面
平面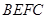 ,
,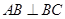 ,得
,得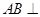 平面
平面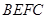 ,
,
从而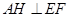 .所以
.所以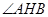 为二面角
为二面角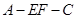 的平面角.
的平面角.
在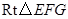 中,因为
中,因为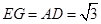 ,
,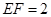 ,
,
所以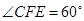 ,
,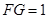 .又因为
.又因为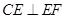 ,所以
,所以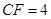 ,
,
从而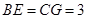 ,于是
,于是 ,
,
因为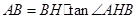 所以当
所以当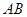 为
为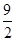 时,
时,
二面角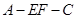 的大小为
的大小为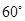 ………12分
………12分

方法二:如图,以点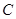 为坐标原点,以
为坐标原点,以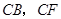 和
和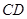 分别作为
分别作为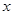 轴,
轴,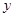 轴和
轴和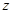 轴,建立空间直角坐标系
轴,建立空间直角坐标系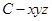 .设
.设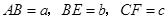 ,
,
则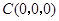 ,
,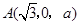 ,
,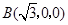 ,
,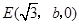 ,
,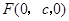 .
.
(Ⅰ)证明: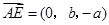 ,
,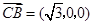 ,
,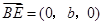 ,
,
所以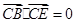 ,
,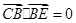 ,从而
,从而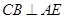 ,
,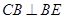 ,
,
所以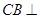 平面
平面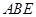 .因为
.因为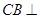 平面
平面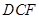 ,所以平面
,所以平面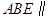 平面
平面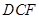 .
.
故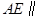 平面
平面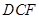 .………6分
.………6分
(Ⅱ)解:因为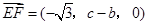 ,
,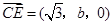 ,所以
,所以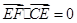 ,
,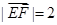 ,从而
,从而
解得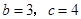 .所以
.所以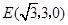 ,
, .设
.设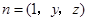 与平面
与平面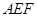 垂直,
垂直,
则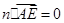 ,
,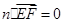 ,解得
,解得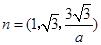 .又因为
.又因为 平面
平面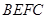 ,
, ,所以
,所以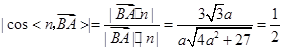 ,
,
得到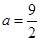 .所以当
.所以当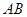 为
为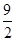 时,二面角
时,二面角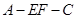 的大小为
的大小为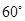 .………12分
.………12分


科目:高中数学 来源:2010-2011学年宁夏高三第五次月考数学理卷 题型:解答题
(本小题满分12分)
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,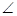 BCF=
BCF=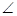 CEF=
CEF= ,AD=
,AD=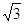 ,EF=2.
,EF=2.
(1)求证:AE//平面DCF;
(2)当AB的长为何值时,二面角A-EF-C的大小为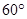 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011年河北省高二下学期期中考试理科数学 题型:解答题
(本小题满分12分)
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,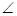 BCF=
BCF=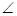 CEF=
CEF=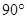 ,AD=
,AD=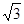 ,EF=2.
,EF=2.

(1)求证:AE//平面DCF;
(2)当AB的长为何值时,二面角A-EF-C的大小为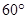 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
(浙江卷理18)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,![]() BCF=
BCF=![]() CEF=
CEF=![]() ,AD=
,AD=![]() ,EF=2。
,EF=2。
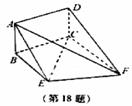 (Ⅰ)求证:AE//平面DCF;
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com