
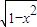 图象上一个动点,过点P作此曲线的切线,其斜率k是t的函数,则函数k=f(t)在(-1,1)上是( )
图象上一个动点,过点P作此曲线的切线,其斜率k是t的函数,则函数k=f(t)在(-1,1)上是( )科目:高中数学 来源: 题型:
 有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,已知AB=4米,AD=2米.
有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,已知AB=4米,AD=2米.查看答案和解析>>
科目:高中数学 来源:2013届黑龙江佳木斯市三校高二下学期期中联考文科数学试卷(解析版) 题型:选择题
已知点P(3,m)在以点F为焦点的抛物线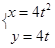 (t为参数)上,则
(t为参数)上,则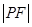 =(
)
=(
)
(A) 1 (B) 2 (C) 3 (D) 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com