
【题目】已知二次函数f(x)=x2+bx+c(其中b,c为实常数).
(1)若b>2,且y=f(sinx)(x∈R)的最大值为5,最小值为﹣1,求函数y=f(x)的解析式;
(2)是否存在这样的函数y=f(x),使得{y|y=x2+bx+c,﹣1≤x≤0}=[﹣1,0],若存在,求出函数y=f(x)的解析式;若不存在,请说明理由.
(3)记集合A={x|f(x)=x,x∈R},B={x|f(f(x))=x,x∈R}.
①若A≠,求证:B≠;
②若A=,判断B是否也为空集.
【答案】
(1)解:由条件知f(x)=x2+bx+c的最大值为5,最小值为﹣1
而b>2,则对称轴 ![]() ,
,
则 ![]() ,即
,即 ![]() ,
,
解得 ![]()
则f(x)=x2+3x+1.
(2)解:f(x)=x2+bx+c,﹣1≤x≤0,对称轴x=﹣ ![]() ,
,
若b≥2,则 ![]() ,则
,则 ![]() ,
,
解得 ![]() ,此时f(x)=x2+2x,
,此时f(x)=x2+2x,
若b≤0,则 ![]() ,则
,则 ![]() ,
,
解得 ![]() ,此时f(x)=x2﹣1,
,此时f(x)=x2﹣1,
若0<b≤1,则 ![]() ,则
,则 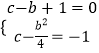 ,
,
解得 ![]() (舍)或
(舍)或 ![]() (舍),
(舍),
此时不存在函数f(x),若1<b<2,则 ![]() ,
,
则 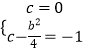 ,解得
,解得 ![]() (舍)或
(舍)或 ![]() (舍),此时不存在函数f(x),
(舍),此时不存在函数f(x),
综上所述存在函数f(x)=x2﹣1和f(x)=x2+2x满足条件
(3)解:由f(x)=x2+bx+c得f(f(x))=f2(x)+bf(x)+c及c=f(x)﹣x2﹣bx,
由f(f(x))=x得到f2(x)+bf(x)+c=x,即f2(x)+bf(x)+f(x)﹣x2﹣bx=x,
整理得到f2(x)﹣x2+b(f(x)﹣x)+(f(x)﹣x)=0,
即(f(x)﹣x)(f(x)+x+b+1)=0①
即f(x)﹣x=0或f(x)+x+b+1=0,
即x2+(b﹣1)x+c=0②或x2+(b+1)x+b+c+1=0③
方程②的判别式△=(b﹣1)2﹣4c
方程③的判别式 ![]() ,
,
①若A≠,即f(x)﹣x=0有解,即x2+(b﹣1)x+c=0有解,即△≥0,则①有解,
即B≠,
②若A=,即△<0,则△1<0,②和③均无解,则①无解,即B=.
【解析】(1)求出函数的对称轴小于﹣1,得到关于b,c的方程组,解出即可;(2)求出f(x)的对称轴,通过讨论对称轴的位置,结合函数的值域求出b,c的值,从而求出f(x)的表达式即可;(3)通过整理方程得到x2+(b﹣1)x+c=0或x2+(b+1)x+b+c+1=0,结合二次函数的性质进行证明即可.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】【2017四川资阳4月模拟】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.
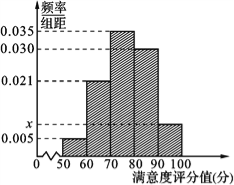
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列
(1)在等差数列{an}中,a6=10,S5=5,求该数列的第8项a8;
(2)在等比数列{bn}中,b1+b3=10,b4+b6= ![]() ,求该数列的前5项和S5 .
,求该数列的前5项和S5 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南通一模19】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若![]() ,证明:函数
,证明:函数![]() 有且只有一个零点;
有且只有一个零点;
(3)若函数![]() 又两个零点,求实数
又两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【南通市、泰州市2017届高三第一次调研测试】(本题满分14分)如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,焦点到相应准线的距离为1.
,焦点到相应准线的距离为1.
(1)求椭圆的标准方程;
(2)若P为椭圆上的一点,过点O作OP的垂线交直线
![]() 于点Q,求
于点Q,求![]() 的值;
的值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②某校高三一级部和二级部的人数分别是m、n,本次期末考试两级部数学平均分分别是a、b,则这两个级部的数学平均分为 ![]() +
+ ![]() ;
;
③某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497﹣﹣512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.
其中命题正确的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E是棱AB上的动点.
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45°,求![]() 的值.
的值.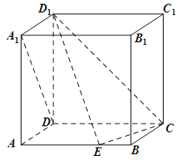
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x2﹣1|+x2+kx.
(1)若对于区间(0,+∞)内的任意x,总有f(x)≥0成立,求实数k的取值范围;
(2)若函数f(x)在区间(0,2)内有两个不同的零点x1 , x2 , 求:
①实数k的取值范围;
② ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公比不为1的等比数列,a1=1,且a1 , a3 , a2成等差数列.
(1)求数列{an}的通项;
(2)若数列{an}的前n项和为Sn , 试求Sn的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com