B
分析:求出两圆的圆心坐标,进而求得两圆的圆心的中垂线的方程,根据直线y=kx+b即为OA的中垂线,求出k与b的值.
解答:圆x
2+y
2+8x-4y=0即(x+4)
2+(y-2)
2=20,表示以A(-4,2)为圆心,以2

为半径的圆.
圆x
2+y
2=20的圆心为O(0,0),半径等于2

,
故OA的中点为C(-2,1),OA的斜率为
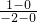
=-

,故OA的中垂线的斜率等于2,
故OA的中垂线的方程为 y-1=2(x+2),即 y=2x+5.
由题意可得,直线y=kx+b即为OA的中垂线,故k与b的值分别等于2和5,
故选B.
点评:本题主要考查圆的标准方程,两圆关于直线对称的性质,属于中档题.
