已知函数f(x)=ax2+bx+c(a,b,c为实数,a≠0),定义域D:[-1,1]
(1)当a=1,b=-1时,若函数f(x)在定义域内恒小于零,求c的取值范围;
(2)当a=1,常数b<0时,若函数f(x)在定义域内恒不为零,求c的取值范围;
(3)当b>2a>0时,在D上是否存在x,使得|f(x)|>b成立?(要求写出推理过程)
解:(1)a=1,b=-1y=x
2-x+c<0在[-1,1]恒成立
则-c>x
2-x在[-1,1]上恒成立
令g(x)=x
2-x,x∈[-1,1],则可得g(x)
max=2
则-c>2即c<-2
(2)a=1,b<0,f(x)=x
2+bx+c≠0在[-1,1]上恒成立?-c≠h(x)=x
2+bx在[-1,1]上恒成立,
而函数h(x)=x
2+bx的对称轴x=
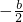
>0
(当
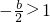
b<-2,函数g(x)在[-1,1]单调递减,则可得g(1)≤g(x)≤g(-1),即1+b≤g(x)≤1-b
所以,-c>1-b或-c<1+b 所以c<b-1或c>-1-b
(II)当
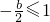
即2≤b<0时,
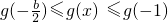
,即
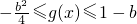
所以
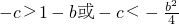
所以,
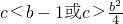
(3)假设在D上存在x,使得|f(x)|>b成立则只要|f(x)|
max>b即可
由于b>2a>0,则对称轴x=-
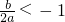
根据二次函数的性质可得|f(x)|的最大值=max{||f(1)|,|f(-1)|}
|a+b+c|>b或|a-b+c|>b
从而可得,存在实数满足条件
分析:(1)a=1,b=-1y=x
2-x+c<0在[-1,1]恒成立,则-c>x
2-x在[-1,1]上恒成立,令g(x)=x
2-x,x∈[-1,1],-c>g(x)
max可求
(2)a=1,b<0,f(x)=x
2+bx+c≠0在[-1,1]上恒成立?-c≠h(x)=x
2+bx在[-1,1]上恒成立,结合函数h(x)的范围可求c得范围
(3)假设在D上存在x,使得|f(x)|>b成立则只要|f(x)|
max>b即可
点评:本题主要考查了二次函数的性质的应用,解题的关键是熟练掌握并能灵活利用二次函数的性质及一定的推理与运算的能力

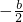 >0
>0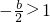 b<-2,函数g(x)在[-1,1]单调递减,则可得g(1)≤g(x)≤g(-1),即1+b≤g(x)≤1-b
b<-2,函数g(x)在[-1,1]单调递减,则可得g(1)≤g(x)≤g(-1),即1+b≤g(x)≤1-b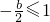 即2≤b<0时,
即2≤b<0时,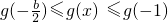 ,即
,即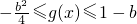
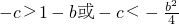
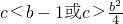
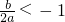


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案