
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
分析 (1)由表中数据得K2≈5.556>5.024,从而根据统计有97.5%的把握认为视觉和空间能力与性别有关.
(2)X的所有可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(1)由表中数据得K2的观测值:
${K^2}=\frac{{50×{{({22×12-8×8})}^2}}}{30×20×30×20}=\frac{50}{9}≈5.556>5.024$.
所以根据统计有97.5%的把握认为视觉和空间能力与性别有关…(6分)
(2)X的所有可能取值为0,1,2,
$P({X=0})=\frac{C_6^2}{C_8^2}=\frac{15}{28},P({X=1})=\frac{C_6^1C_2^1}{C_8^2}=\frac{3}{7},P({X=2})=\frac{C_2^2}{C_8^2}=\frac{1}{28}$.
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{15}{28}$ | $\frac{3}{7}$ | $\frac{1}{28}$ |
点评 本题考查独立检验的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
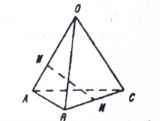
如图,空间四边形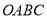 中,
中,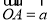 ,
,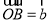 ,
,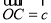 ,点
,点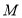 在
在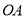 上,且
上,且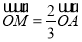 ,点
,点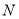 为
为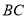 中点,则
中点,则 等于( )
等于( )
A.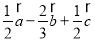 B.
B.
C.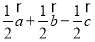 D.
D.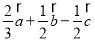
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,2\root{3}{3})$ | B. | $(2\root{3}{3},+∞)$ | C. | $(-2\root{3}{3},2\root{3}{3})$ | D. | $(0,2\root{3}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 0.9 | 1.9 | 3.2 | 4.4 |
| A. | 0.6 | B. | 0.7 | C. | 0.8 | D. | 0.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车间 | 每辆童车所需的加工工时 | 有效工时(小时/日) | |
| A | B | ||
| 机械 | 0.8 | 1.2 | 40 |
| 油漆 | 0.6 | 0.8 | 30 |
| 装配 | 0.4 | 0.6 | 25 |
| 利润(元/辆) | 6 | 10 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{3},\frac{1}{2})$ | B. | $(\frac{1}{2},1)$ | C. | $(\frac{1}{3},1)$ | D. | $(-\frac{1}{3},\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com