
分析 (Ⅰ)设A(x0,y0),B(x,y),由题意可得可得$\left\{\begin{array}{l}{{x}_{0}=x}\\{{y}_{0}=2y}\end{array}\right.$,代入x2+y2=4化简可得;
(Ⅱ)由向量式可得$\overrightarrow{PM}$=4$\overrightarrow{PN}$,当直线l的斜率不存在时x=0符合题意;
当直线l的斜率存在时,设直线l的方程为y=kx+$\frac{5}{3}$,代入$\frac{{x}^{2}}{4}$+y2=1消y由韦达定理可得关于k的方程,化简可得矛盾,综合可得所求直线为x=0
解答 解:(Ⅰ)设A(x0,y0),B(x,y),
由$\left\{\begin{array}{l}{x={x}_{0}}\\{y=\frac{1}{2}{y}_{0}}\end{array}\right.$可得$\left\{\begin{array}{l}{{x}_{0}=x}\\{{y}_{0}=2y}\end{array}\right.$,
代入x2+y2=4化简可得$\frac{{x}^{2}}{4}$+y2=1
∴曲线C的方程为$\frac{{x}^{2}}{4}$+y2=1,是焦点在x轴的椭圆;
(Ⅱ)∵$\overrightarrow{QM}$=$\overrightarrow{4QN}$-$\overrightarrow{3QP}$,∴$\overrightarrow{PM}$=4$\overrightarrow{PN}$,①
当直线l的斜率不存在时,M(0,-1),N(0,1),此时直线方程为x=0符合题意;
当直线l的斜率存在时,设直线l的方程为y=kx+$\frac{5}{3}$,
代入$\frac{{x}^{2}}{4}$+y2=1消y并整理可得(9+36k2)x2+120kx+64=0,
由△=14400k-256(9+36k2)>0可解得k2>$\frac{4}{9}$,
设M(x1,y1),N(x2,y2),
则由韦达定理可得x1+x2=-$\frac{120k}{9+36{k}^{2}}$,②
x1x2=$\frac{64}{9+36{k}^{2}}$,③
由①得x1=4x2,④
由②③④消去x1,x2可得$\frac{16}{9+36{k}^{2}}$=$\frac{24{k}^{2}}{(9+36{k}^{2})^{2}}$,
即$\frac{36{k}^{2}}{9+36{k}^{2}}$=1无解,
综上可得存在符合条件的直线x=0
点评 本题考查直线与圆锥曲线的综合问题,涉及椭圆方程的求解和圆锥曲线设而不求的思想以及分类讨论,属难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相关指数R2为0.95的模型 | B. | 相关指数R2为0.81的模型 | ||
| C. | 相关指数R2为0.50的模型 | D. | 相关指数R2为0.32的模型 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
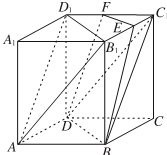 正方体ABCD-A1B1C1D1中,E,F分别为棱B1C1,C1D1的中点,
正方体ABCD-A1B1C1D1中,E,F分别为棱B1C1,C1D1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [0,+∞) | C. | (0,+∞) | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com