练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．若复数z=（1+ai）（1-i）为纯虚数，i是虚数单位，则实数a的值是-1，|$\overline{z}+i$|=3．

    分析 直接由复数代数形式的乘法运算化简复数z，再由已知条件列出方程组，求解得a的值，再求出$\overline{z}$，由复数求模公式计算得答案．

    解答 解：∵z=（1+ai）（1-i）=a+1+（a-1）i为纯虚数，
    ∴$\left\{\begin{array}{l}{a+1=0}\\{a-1≠0}\end{array}\right.$，
    解得a=-1．
    ∴z=-2i，则$\overline{z}=2i$．
    ∴|$\overline{z}+i$|═|2i+i|=|3i|=3．
    故答案为：-1，3．

    点评 本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=2$\sqrt{3}sin\frac{ωx}{2}cos\frac{ωx}{2}+6{cos^2}\frac{ωx}{2}$-3（ω＞0）
    （1）若$y=f（x+θ）（0＜θ＜\frac{π}{2}）$是最小正周期为π的偶函数，求ω和θ的值；
    （2）若g（x）=f（3x）在$（0，\frac{π}{3}）$上是增函数，求ω的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

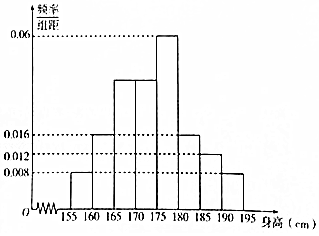    12．从某校高一年级1000名学生中随机抽取100名测量身高，测量后发现被抽取的学生身高全部介于155厘米到195厘米之间，将测量结果分为八组：第一组[155，160），第二组[160，165），…，第八组[190，195），得到频率分布直方图如图所示．
    （Ⅰ）计算第三组的样本数；并估计该校高一年级1000名学生中身高在170厘米以下的人数；
    （Ⅱ）估计被随机抽取的这100名学生身高的中位数、平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设a，b，c是三条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是（　　）
    A．若α⊥β，α⊥γ，则β⊥γB．若a，b与c所成的角相等，则a∥b
    C．若α⊥α，α∥β，则α⊥βD．若a∥b，a?α，则b∥α

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

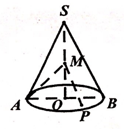    16．如图，圆锥的轴截面SAB是正三角形，O为底面中心，M为线段SO中点，动点P在圆锥底面内（包括圆周），若AM⊥MP，则点P的轨迹为（　　）
    A．线段B．圆C．椭圆D．抛物线

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

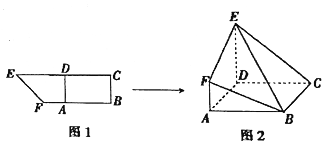    6．如图所示，在直角梯形BCEF中，∠CBF=∠BCE=90°，A，D分别是BF，CE上的点，AD∥BC，且AB=DE=2BC=2AF（如图1），将四边形ADEF沿AD折起，连结BE、BF、CE（如图2）．在折起的过程中，下列结论错误的是④．（填序号）
    ①AC∥平面BEF；
    ②B、C、E、F四点不可能共面；
    ③若EF⊥CF，则平面ADEF⊥平面ABCD；
    ④直线EF与AC所成角可能为15°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若等边三角形ABC的边长为4，E是中线BD的中点，则$\overrightarrow{AE}$•$\overrightarrow{EC}$=（　　）
    A．1B．-1C．2D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设函数f（x）在（-∞，+∞）上有意义，对于给定的正数k，定义函数fk（x）=$\left\{\begin{array}{l}{f（x），f（x）＜k}\\{k，f（x）≥k}\end{array}\right.$取k=3，f（x）=（$\frac{k}{2}$）|x|，则fk（x）=$\frac{k}{2}$的零点有（　　）
    A．0个B．1个
    C．2个D．不确定，随k的变化而变化

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设函数f（x）=ax-（k+1）a-x（a＞0且a≠1）是定义在R上的奇函数．
    （1）求k的值；
    （2）若f（1）=$\frac{3}{2}$，且g（x）=a2x+a-2x-2mf（x）在[0，+∞）上的最小值为-6，求m的值．

    查看答案和解析>>

    同步练习册答案