
【题目】已知圆C:x2+y2=4,直线l:y+x﹣t=0,P为直线l上一动点,O为坐标原点.
(1)若直线l交圆C于A、B两点,且∠AOB= ![]() ,求实数t的值;
,求实数t的值;
(2)若t=4,过点P做圆的切线,切点为T,求 ![]()
![]() 的最小值.
的最小值.
【答案】
(1)解:∵圆C:x2+y2=4,直线l:y+x﹣t=0,P为直线l上一动点,O为坐标原点.
直线l交圆C于A、B两点,且∠AOB= ![]() ,
,
∴圆心到直线l的距离为1,
即圆心(0,0)到直线l的距离d= ![]() =1,
=1,
解得t= ![]()
(2)解:∵t=4,过点P做圆的切线,切点为T,
∴ ![]()
![]() =|
=| ![]() ||
|| ![]() |cosθ=|
|cosθ=| ![]() |2=|
|2=| ![]() |2﹣4,
|2﹣4,
∴求 ![]()
![]() 的最小值.等价于求|
的最小值.等价于求| ![]() |2﹣4的最小值,
|2﹣4的最小值,
∵| ![]() |的最小值d=
|的最小值d= ![]() =2
=2 ![]() ,
,
∴ ![]()
![]() 的最小值为(2
的最小值为(2 ![]() )2﹣4=4
)2﹣4=4
【解析】(1)由∠AOB= ![]() ,得到圆心到直线l的距离为1,由此求出圆心(0,0)到直线l的距离
,得到圆心到直线l的距离为1,由此求出圆心(0,0)到直线l的距离 ![]() =1,从而能求出t.(2)
=1,从而能求出t.(2) ![]()
![]() =|
=| ![]() ||
|| ![]() |cosθ=|
|cosθ=| ![]() |2=|
|2=| |2﹣4,求出|
![]() |的最小值d=2
|的最小值d=2 ![]() ,由此能求出
,由此能求出 ![]()
![]() 的最小值.
的最小值.
【考点精析】关于本题考查的直线与圆的三种位置关系,需要了解直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
A.f(x)=x3
B.f(x)=x ![]()
C.f(x)=3x
D.f(x)=( ![]() )x
)x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
①当切线在两坐标轴上的截距为零时,设切线方程为y=kx,
则 ![]() ,解得k=2±
,解得k=2± ![]() ,
,
从而切线方程为y=(2± ![]() )x.
)x.
②当切线在两坐标轴上的截距不为零时,设切线方程为x+y-a=0,则 ![]() ,解得a=-1或3,
,解得a=-1或3,
从而切线方程为x+y+1=0或x+y-3=0.
综上,切线方程为(2+ ![]() )x-y=0或(2-
)x-y=0或(2- ![]() )x-y=0或x+y+1=0或x+y-3=0
)x-y=0或x+y+1=0或x+y-3=0
(2)点P在直线l:2x-4y+3=0上,过点P作圆C的切线,切点记为M,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①整数集可以表示为{x|x为全体整数}或{ ![]() };
};
②方程组 ![]() 的解集为 {x=3,y=1};
的解集为 {x=3,y=1};
③集合{x∈N|x2=1}用列举法可表示为{1,1};
④集合 ![]() 是无限集.
是无限集.
其中正确的是 ( )
A.①和③
B.②和④
C.④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x ![]() )﹣2sin(x
)﹣2sin(x ![]() )cos(x
)cos(x ![]() )
)
(1)求函数f(x)的最小正周期; (Ⅱ)求函数f(x)在区间[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个圆锥形的空杯子上放着一个直径为8cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?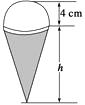
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com